Rumo à Internet Física: modularidade dos serviços logísticos e implicações de projeto
- internet física
- logística de embalagens
- desequilíbrios de frete
- modularização de serviço
- programação linear
INTRODUÇÃO
Os desafios econômicos, sociais e, talvez o mais importante, ambientais das cadeias de suprimentos atuais exigem novas abordagens para a gestão da cadeia de suprimentos (Montabon et al. 2016). O sucesso de projetos de colaboração horizontal como o CO3 (Projeto CO3 2014) e projetos de colaboração liderados pela indústria (Creemers et al. 2017) inspirou o desenvolvimento da Internet Física (PI ou π; Montreuil 2011; Mervis 2014). A PI é um conceito inovador que utiliza a Internet Digital como metáfora para recursos compartilhados, como transporte e armazenagem, com o frete encapsulado em PI-containers (Landschutzer et al. 2015; MODULUSHCA 2016) e transportado por meio de um protocolo padrão (Montreuil et al. 2012; Ballot et al. 2014). Comparado com o sistema logístico convencional, a PI representa um sistema radicalmente diferente (Ballot et al. 2014; Ambra et al. 2020) que forçará as partes interessadas privadas e públicas a repensarem suas estratégias de cadeia de suprimentos.
Principais formuladores de políticas, como a Comissão Europeia, adotaram a PI como a visão alvo para a logística europeia em 2050; mundialmente, grandes partes interessadas da indústria, associações e autoridades estão aderindo à iniciativa estratégica ALICE[1] em um esforço para difundir a Internet Física (Pan et al. 2017; ALICE 2019; Ambra et al. 2019). Vários estudos destacaram enormes potenciais melhorias tanto pelo conceito da PI quanto pela área adjacente de compartilhamento de transporte e armazenagem (Pan et al. 2013; Creemers et al. 2017). Ballot et al. (2012) relataram uma redução de 20% no consumo de combustível; Sarraj et al. (2014a) observaram uma possível redução de 60% de CO2; e Yang et al. (2017) mostraram que o custo logístico poderia, em alguns casos, ser reduzido em até 73%. Como a Internet Física promete melhorar a sustentabilidade econômica, ambiental e social e atrair investimentos públicos e privados significativos, sua adoção e efeitos antecipados são altamente relevantes para profissionais, formuladores de políticas e acadêmicos (Sternberg e Norrman 2017; ALICE 2019).
A automação de terminais (ou seja, carregamento e descarregamento automatizados) possibilita um novo paradigma de design da rede da cadeia de suprimentos, já que os profissionais da cadeia de suprimentos atualmente tentam evitar os riscos e desperdícios associados ao carregamento e descarregamento (Hübner e Ostermeier 2019). Atualmente, a falta de embalagens padronizadas, como os contêineres PI, é uma barreira para a automação de terminais, dificultando potenciais ganhos de eficiência (Mervis 2014; Montreuil et al. 2015).
De acordo com Montreuil et al. (2015), “O Physical Internet lida estritamente com mercadorias encapsuladas em π-contêineres modulares padrão que devem ser o equivalente material aos [pacotes de dados da Internet Digital]” (p.2). Os contêineres PI estarão disponíveis em muitas variações e tamanhos, acomodando virtualmente todos os tipos de produtos (Montreuil et al. 2013) e unidades de carga. A capacidade de uma cadeia de suprimentos de reposicionar ou carregar de volta embalagens retornáveis, como um contêiner PI, depende em grande medida das características da embalagem retornável. Embalagens com características específicas que as tornem incompatíveis com o carregamento de outros tipos de mercadorias causarão aumento de viagens vazias (McKinnon e Ge 2006). Considerando que os contêineres PI são de tamanhos diferentes e não roteados centralmente, Sternberg e Norrman (2017) enfatizam a importância estratégica de analisar o efeito dos múltiplos contêineres PI nos balanços de frete, pois o reposicionamento de embalagens retornáveis ou qualquer tipo de contêiner é crucial para estimar com precisão os ganhos de eficiência (Mollenkopf et al. 2005; Kolar et al. 2018; Kuzmicz e Pesch 2019).
Apesar do potencial e das pesquisas significativas sobre o PI (Ballot et al. 2016), Treiblmaier et al. (2016) destacam que as pesquisas sobre a Internet Física geralmente falharam em incorporar teoria e que a base teórica é “altamente subdesenvolvida” (p. 15). Pelo que sabemos, os protocolos detalhados, pacotes (contêineres PI) e interfaces definidos nos projetos do PI (cf., Meller et al. 2013; Ballot et al. 2014) fazem dele a modularização de serviço mais amplamente especificada (Starr 2010) conhecida na área de gestão da cadeia de suprimentos.
O objetivo deste artigo foi analisar os contêineres PI sob uma perspectiva logística estratégica (Bartolacci et al. 2012). Baseamo-nos na teoria da modularidade de serviços para enquadrar os antecedentes dos efeitos futuros da Internet Física, respondendo a várias demandas de pesquisa sobre a Internet Física (Treiblmaier et al., 2020; Pan et al. 2017; Sternberg e Norrman 2017; Ambra et al. 2019).
Dado que o objetivo da Internet Física é enfrentar o grande desafio da sustentabilidade na logística (Montreuil 2011), o efeito do reposicionamento dos contêineres PI determina benefícios futuros, um fator crucial que influencia a intenção de adotar estrategicamente uma nova inovação (Premkumar et al. 1997; Venkatesh et al. 2003). Assim, como ponto de partida para investigar os efeitos das características dos contêineres PI, apresentamos a seguinte questão de pesquisa: Quais são as implicações da modularidade do serviço da Internet Física nos fluxos de contêineres PI? Em outras palavras, como o nível de modularidade do serviço (ou compatibilidade dos contêineres PI no transporte regional) afeta os fluxos dos contêineres PI e, mais especificamente, o reposicionamento dos contêineres PI? Contribuímos para as discussões em andamento com insights tanto para formuladores de políticas quanto para pesquisadores da cadeia de suprimentos nas áreas de estratégia da Internet Física e teoria contextualizada de médio alcance (Stank et al. 2017) da modularização de serviços logísticos (Voss et al. 2016). Além disso, ampliamos a literatura tradicional sobre reposicionamento de contêineres marítimos, detalhando as especificidades dos contêineres PI. Como a Internet Física ainda não existe, esta pesquisa é conceitual; no entanto, utilizamos dados empíricos em um modelo de programação linear para analisar os efeitos esperados, uma abordagem metodológica comumente usada para o reposicionamento de contêineres marítimos (Shintani et al. 2007; Kuzmicz and Pesch 2019). A teoria Geral de Sistemas Modulares de Schilling (2000) é usada para enquadrar os resultados.
O foco deste artigo é a modularidade e a logística de embalagens (entrada no sistema modular) no transporte intra-regional de carga geral, ou seja, transporte terminal a terminal. Assim, os problemas da primeira e última milha estão fora do escopo deste artigo. Como será discutido, examinamos os efeitos logísticos estratégicos em um sistema híbrido (Fazili et al. 2017), focando no nível estratégico da demanda, oferta e transporte. Como apenas cerca de 1% da carga geral na Suécia é transportada por ferrovia (Sandberg et al. 2016), nossa análise foca no transporte rodoviário de carga geral. Nossos resultados destacam a importância da manutenção da modularidade do serviço no sistema de transporte, mostrando que a carga conjunta na Internet Física representa uma melhoria de eficiência, compensando o material adicional de embalagem a ser transportado. Contudo, nossos resultados também ressaltam que, se a modularidade do serviço for reduzida pela falta de compatibilidade da embalagem de transporte, os ganhos de eficiência deixam de se materializar. Isso é de grande importância para estratégias futuras de SCM e formulação de políticas, pois enfatiza as condições em que a Internet Física faz parte da solução para o grande desafio.
LITERATURA RELACIONADA
Esta seção descreve alguns dos conceitos relacionados ao PI: logística de embalagens e taxas de preenchimento, os componentes do PI e a modelagem do reposicionamento de contêineres marítimos. Para uma discussão mais extensa ou geral do conceito, consulte o livro de Ballot et al. (2014) sobre PI ou a recente revisão da literatura de Treiblmaier et al. (2020).
Logística de embalagens e taxas de preenchimento
Embalagem geralmente se refere a diferentes níveis de embalagem no sistema logístico. A embalagem primária está mais próxima do produto e é frequentemente a embalagem para o consumidor ou para vendas. A embalagem secundária contém um determinado número de embalagens primárias, frequentemente denominada embalagem varejista. A embalagem terciária contém vários itens de embalagem secundária, frequentemente referida como embalagem de transporte, como um euro-palete. A logística de embalagens foca nas sinergias alcançadas pela integração dos sistemas de embalagem e logística (Pålsson and Hellström 2016).
Fluxos de transporte equilibrados são uma das chaves para altas taxas de preenchimento e transporte de carga sustentável, porém desequilíbrios de carga caracterizam a logística na maior parte do mundo (Hesse e Rodrigue 2004). Fluxos desequilibrados e viagens a vazio são ainda mais comuns em certas partes do processo de distribuição, como a logística do primeiro e último quilômetro. Em distâncias maiores, equilibrar os fluxos torna-se mais importante. Por exemplo, na Escandinávia, os fluxos norte-sul e sul-norte na Noruega, Suécia e Finlândia diferem amplamente em termos de volume e tipos de mercadorias transportadas (Vierth et al. 2012; Wall 2013). Portanto, ser capaz de transportar diferentes tipos de mercadorias dependendo da direção dos fluxos inter-regionais é crucial. McKinnon e Ge (2006) analisaram o potencial de backhauling no Reino Unido e descobriram que a incompatibilidade entre veículos e produtos (ou seja, a embalagem) foi um dos principais fatores por trás das viagens a vazio.
Componentes da internet física
De acordo com pesquisadores como Ambra et al. (2019) e Matusiewicz (2020), a Internet Física, a visão para a logística até 2050, contém um roteiro detalhado do desenvolvimento do conceito e marcos significativos através da ALICE (2019). Nesta seção, elaboramos sobre a infraestrutura da Internet Física e os contêineres da Internet Física.
Infraestrutura PI
Ambra et al. (2019) descrevem a mecânica da Internet Física da seguinte forma: “A PI é inspirada na metáfora da Internet Digital que utiliza comutação de pacotes; a mensagem é dividida em diferentes pedaços (pacotes) que viajam pela internet por várias rotas e são reunidos no lado do receptor. Os pacotes são roteados por meio de uma rede interconectada de nós/hubs (PI-hubs) dependendo da capacidade da rede. Essa abordagem de desmontagem está sendo adaptada pela PI, onde as mercadorias físicas ou, em sentido mais geral, objetos físicos podem ser encaminhados por diferentes vínculos desde suas origens até os destinos em contêineres padronizados usando procedimentos de manuseio padronizados” (p. 1607).
Diversos artigos sobre PI abordaram protocolos (Montreuil et al. 2012; Sarraj et al. 2014a) e roteamento (Ballot et al. 2012; Sarraj et al. 2014b). Como todos os hubs serão interoperáveis, uma vantagem distinta da Internet Física seria que praticamente todas as rotas poderiam ser trafegadas por caminhões cheios, uma grande razão para as melhorias do conceito em relação aos sistemas convencionais anteriormente descritas. Os PI-hubs são projetados para lidar automaticamente com os PI-contêineres de entrada e saída (Veja Figura 1; Ballot et al. 2013).
Devido ao seu manuseio rápido e autônomo previsto, as janelas de tempo perdem sua importância relativa (cf. como a Internet Digital transporta pacotes de dados), porque as restrições no transporte terminal a terminal só se tornam uma preocupação significativa quando as mercadorias estão indo de um terminal para um destinatário.
Contêineres PI (PI-containers)
O sistema de contêineres PI é uma parte integral da Internet Física (Montreuil 2011; Ballot et al. 2014). Todas as mercadorias são embaladas em contêineres PI, que são empilháveis e podem ser manuseados em PI-hubs automatizados (Montreuil et al. 2013). Sallez et al. (2016) descrevem as três principais categorias de contêineres PI. Os contêineres de embalagem, os mais próximos do produto, são as embalagens primárias. Contêineres de manuseio contêm um produto individual, um agrupamento de produtos ou vários contêineres de embalagem (embalagem secundária). Finalmente, contêineres de transporte contêm os contêineres de manuseio para transporte (embalagem terciária). Presume-se que os contêineres PI substituam os paletes nos quais diferentes tipos de carga podem ser carregados. Bonecas russas são frequentemente usadas para ilustrar o aninhamento dos contêineres PI (Montreuil 2011).
O artigo de Landschutzer et al. (2015) e o relatório final do projeto MODULUSHCA da Comissão Europeia (2016) descrevem dois casos de contêineres PI: o contêiner de manuseio denominado m-box (ver Figura 2) e o contêiner de transporte referido como contêiner PI de carga unitária. As m-boxes são carregadas dentro do contêiner PI de carga unitária, e esses contêineres são carregados em um trailer padrão europeu (Landschutzer et al. 2015). A m-box do projeto MODULUSHCA se encaixa em trailers padrão europeus (padrão europeu com comprimento máximo de 16,5 m, peso máximo (caminhão + trailer) de 40 toneladas). Entretanto, se usadas com TEUs, o uso das caixas geraria muito espaço ocioso (devido à incompatibilidade inerente entre paletes EU e TEUs), uma questão que permanece sem solução.


Embora as m-boxes atualmente não sejam dobráveis, a função de dobragem é esperada para a próxima geração (MODULUSHCA 2016). Contêineres PI dobráveis são compatíveis, pois os contêineres PI dobrados podem ser reposicionados com qualquer categoria de mercadorias.
A literatura sugere dimensões adicionais possíveis para contêineres PI, que se pressupõe serem empilháveis, permitindo altas taxas de preenchimento dos contêineres PI de carga unitária. Sarraj et al. (2014a) propõem um conjunto de contêineres PI modulares com diferentes tamanhos (2,4 m * 2,4 m * [1,2, 2,4, 3,6, 4,8, 6, 12] m). Essa modularidade é baseada no contêiner “pallet-wide” (PW), que é uma unidade de transporte intermodal usada na Europa. Segundo Sarraj et al. (2014a), esses tamanhos representam tamanhos potenciais. Utilizando esses tamanhos, eles apresentam uma formulação do Problema de Empacotamento de Caixas (Bin Packing Problem - BPP) para embalar os contêineres PI por modos de transporte (por exemplo, caminhões) (Sarraj et al. 2014a).
Para estudar problemas de interrupção em hubs PI, Yang et al. (2017) utilizaram os mesmos tamanhos de contêiner PI e protocolos de empacotamento dos contêineres PI (especificando como atribuir cargas a um contêiner PI com melhor ajuste). Hauder et al. (2018) também sugerem o uso do problema BPP para atribuir contêineres PI a transportadores PI (modos de transporte).
Reposicionamento de contêineres
Desbalanceamentos de fluxo entre diferentes regiões na rede e a necessidade resultante de equilibrar os fluxos de contêineres PI são esperados como em qualquer sistema. No PI, espera-se que os contêineres sejam comumente usados por todas as empresas de navegação. Portanto, o reposicionamento de contêineres PI é, em teoria, mais fácil, mas necessário devido aos tipos de carga incompatíveis e desequilíbrios comerciais entre as áreas geográficas onde os hubs do PI estão localizados. O estudo recente de Kolar et al. (2018), baseado em um estudo de caso no país sem litoral da República Tcheca, sugere que, na prática, o reposicionamento de contêineres vazios é percebido mais como um problema de desequilíbrio comercial global do que como um problema de alocação integrada de recursos ou equipamentos e roteamento de veículos. Devido a essa percepção, as transportadoras marítimas concentram-se principalmente em soluções em nível global, e não regional. Na literatura, diferentes aspectos do problema de reposicionamento de contêineres vazios foram abordados usando modelagem matemática e programação linear ou estocástica (por exemplo, Yun et al. 2001; Jula et al. 2006; Song 2007). Kuzmicz e Pesch (2019) fornecem uma revisão detalhada das abordagens de otimização para o problema em termos do reposicionamento de contêineres TEU e FEU.
A programação linear, que é uma das abordagens comumente usadas (Kuzmicz e Pesch 2019), assume demandas determinísticas e fornece soluções de custo mínimo para reposicionamento sob diferentes políticas de reutilização de contêineres. No contexto do PI, o reposicionamento de contêineres vazios também pode apresentar um problema em termos dos contêineres PI. Embora se assuma que os contêineres PI venham em diferentes tamanhos, tipos de carga incompatíveis e desequilíbrios comerciais ainda podem tornar necessário o reposicionamento vazio dos contêineres PI. Considerando a compatibilidade dos contêineres PI na capacidade de conter (ou serem transportados junto com) diferentes tipos de carga, estudamos quanto reposicionamento vazio de contêineres PI seria necessário sob diferentes cenários de compatibilidade. Conforme articulado em Rogers et al. (2012), a programação linear é adequada para a análise de cenários por meio da alteração dos parâmetros de interesse.
QUADRO TEÓRICO: MODULARIDADE EM SERVIÇOS LOGÍSTICOS
A modularidade é considerada uma forma de aumentar a comunalidade entre diferentes versões ou variantes de produto dentro de um sistema ou de uma família de produtos, ou seja, permitir que os mesmos componentes sejam usados em várias variantes de produto (Schilling 2000; Salvador et al. 2002). Um sistema pode ser definido não apenas no nível da indústria ou da organização, mas também no nível de um produto (bem ou serviço) a ser fornecido ao cliente (Schilling 2000). Tuunanen et al. (2012) definem um módulo de serviço como “um sistema de componentes que oferece uma funcionalidade bem definida por meio de uma interface precisamente descrita e com o qual um serviço modular é composto, adaptado, personalizado e individualizado” (p. 102).
As interfaces são os mecanismos que integram os subsistemas em um todo. Nesse sentido, as interfaces asseguram o acoplamento frouxo, o que permite que os subsistemas funcionem independentemente e possibilita a substituição de subsistemas conforme necessário para alterar o próprio sistema. Salvador et al. (2002) explicam: “Como tal, uma das motivações que fundamenta a linha de pesquisa em gestão de operações tem sido entender os benefícios da comunalidade de componentes sobre o desempenho operacional, bem como os diversos fatores que podem afetar esses benefícios” (p. 551).
Schilling (2000) delineou um modelo para descrever os fatores que impulsionam a integração (diminuição da modularidade) e a desagregação (aumento da modularidade): “Em seu nível mais abstrato, ela (modularidade) refere-se simplesmente ao grau em que os componentes de um sistema podem ser separados (separabilidade) e recombinados” (p. 315). O quadro de modularidade de Schilling contém os seguintes componentes:
- Heterogeneidade das entradas refere-se a quão fácil ou difícil é modularizar o sistema. As entradas em um sistema de serviço incluem tanto as opções tecnológicas disponíveis para alcançar funções específicas quanto os recursos e capacidades das empresas envolvidas na produção do serviço. Por exemplo, as características do óleo quente em grande volume e do peixe congelado são muito diferentes. Essas entradas heterogêneas exigem equipamentos de transporte especializados (tanque de alimentos e trailer congelador, respectivamente), tornando-as difíceis de modularizar. No entanto, no cenário do óleo quente em grande volume e do peixe congelado, se um sistema modular fosse capaz de manusear essas entradas heterogêneas no mesmo sistema, tal sistema poderia concretizar ganhos significativos de eficiência no transporte.
- Heterogeneidade das demandas refere-se ao nível de diferenças entre as demandas dos clientes. Quanto mais semelhantes forem as demandas dos clientes, mais o sistema tende a aumentar a modularização.
- A especificidade sinérgica do sistema cria pressão contrária à migração do sistema para a modularidade. Entradas heterogêneas em combinação com demandas heterogêneas reforçarão o efeito uma da outra, criando especificidade sinérgica que leva a menos modularidade.
- Urgência refere-se à mudança tecnológica (ou à sua velocidade) e à intensidade competitiva. Fabricantes com vendas pós-mercado lucrativas tentarão manter o status quo e atuar contra a modularização. Por outro lado, autoridades como a Comissão Europeia tentarão impor a modularidade por meio de interfaces abertas e padrões (por exemplo, Comissão Europeia 2016).
Schilling (2000) também argumenta que sistemas em geral são caracterizados por inércia e que não respondem imediatamente e de forma vigorosa. Revisitando mais de 45 anos de modularidade no campo da gestão de operações, Starr (2010) explica que a modularização na indústria manufatureira não atingiu a adoção antecipada porque a fabricação de baixo custo no exterior representava uma economia relativamente maior para a indústria. Contudo, a modularização no contexto dos serviços de transporte geralmente não requer alterações de engenharia nos produtos, embora exceções existam e possam ser altamente benéficas (Hellström e Nilsson 2011). Embora essas mudanças possam se tornar muito custosas, elas alteram os meios pelos quais os produtos são manuseados e transportados. Os PI-containers e PI-hubs da Internet Física podem fornecer esses meios.
Schilling (2000) define a ação principal para aumentar a modularidade como a capacidade de combinar e recombinar entradas heterogêneas em uma variedade de configurações heterogêneas e sugere que “⋯, a heterogeneidade na gama de entradas, combinada com a heterogeneidade dos clientes, cria incentivos poderosos para adotar um sistema modular” (p. 317). No contexto de um sistema logístico, devido à heterogeneidade das entradas (mercadorias), diferentes embalagens ou contêineres são usados. Essas embalagens específicas para as mercadorias podem ser consideradas componentes de um sistema modular que podem ser separados e recombinados. Por exemplo, o conteúdo de um contêiner (pacotes ou PI-containers) entregue a um hub pode ser separado e enviado do hub para outro hub ou para seus destinos finais. Em contraste com a modularidade de produtos, a modularidade de serviços geralmente não corre o risco de perder nenhuma funcionalidade de transporte porque é comoditizada e porque a maioria dos recebedores de mercadorias tem demandas homogêneas.
Por outro lado, a especificidade sinérgica, como fator esperado para diminuir a modularidade, pode ser um obstáculo quando pacotes com a mesma etiqueta de origem e destino não podem ser eficazmente combinados na mesma unidade de carga. Por exemplo, suponha que um PI-container, como um tambor de óleo, seja criado para encapsular um tipo de mercadoria.
Esses contêineres PI para tambores devem ser devolvidos a um local de produção após o óleo ter sido consumido no local da demanda. Se o local produz bens embalados em contêineres PI (como caixas m-box) que não podem ser dobrados, a cadeia de suprimentos enfrenta um fluxo duplo de mercadorias porque o reposicionamento respectivo de cada tipo de contêiner PI seria incompatível com o fluxo regular, ou seja, gerando um desequilíbrio de frete porque o reposicionamento dos contêineres PI não é separável. Portanto, se os fluxos de contêineres PI tiverem baixo nível de compatibilidade, é improvável que a Internet Física seja a estratégia escolhida pelos remetentes, que não desejariam pagar uma cobrança extra pelo reposicionamento dos contêineres PI vazios (ou seja, o baixo nível de compatibilidade representa especificidade sinérgica).
De acordo com o framework de Schilling (2000), urgência é o último fator que afeta a adoção da modularidade. Na logística, a urgência decorre das demandas de sustentabilidade ambiental e social que pressionam os transportadores a mudar seus métodos. A urgência também é possibilitada e motivada por mudanças tecnológicas, como computação em nuvem e Internet das Coisas. É importante notar que a modularidade na Internet Física é paradoxal, pois os contêineres PI, embora claramente exemplifiquem a modularização, também apresentam o risco de amplificar a heterogeneidade das entradas. Com o aumento da heterogeneidade das entradas (causando fluxos incompatíveis de contêineres PI), a modularidade do serviço pode ser negativamente afetada. Neste manuscrito, investigamos o efeito desses fatores nos fluxos de contêineres PI da Internet Física. Assumimos que a heterogeneidade em termos tanto de entradas quanto de saídas (demanda do cliente) permanece constante na indústria logística. Portanto, focamos na especificidade sinérgica em termos de compatibilidade dos contêineres PI e na urgência em termos do uso de tecnologia e sustentabilidade ambiental.
DESENHO DA PESQUISA
No contexto da modularização de serviços e da logística de embalagens, nosso estudo utiliza modelagem matemática para abordar os efeitos estratégicos logísticos dos fluxos de contêineres PI da Internet Física. Com trabalhos extensivos realizados em alguns aspectos do conceito, mas muito pouco sobre contêineres PI (Treiblmaier et al., 2020; Sternberg e Norrman 2017) e pesquisas anteriores sobre reposicionamento de contêineres marítimos, o estado atual do PI sugere que elaborar sobre os efeitos do reposicionamento do sistema de contêineres PI usando modelagem matemática é adequado (Shintani et al. 2007; Rogers et al. 2012; Kuzmicz e Pesch, 2019).
Este artigo oferece uma análise estratégica dos volumes totais e equilíbrios de frete e contêineres PI em uma rede terminal a terminal. Os resultados têm a intenção de oferecer implicações estratégicas sobre os efeitos da adoção do PI para gerentes da cadeia de suprimentos e formuladores de políticas. Assim, nosso modelo determinístico não examina operações, sazonalidade e outros fatores temporais, mas sim foca na questão mais importante (do ponto de vista da adoção) do efeito geral das características do contêiner PI. Conforme destacado por Waller e Fawcett (2012), um desafio na aplicação de modelagem matemática para gerar teoria em cadeia de suprimentos e logística tem sido frequentemente que as implicações e pressupostos tornaram os modelos menos úteis ou impraticáveis. Para superar esse desafio, consultamos vários especialistas e profissionais da indústria logística e observamos cuidadosamente os fluxos do estudo que estão sendo modelados. Os resultados dessas consultas formam as premissas desta pesquisa. Contudo, antes de descrever o modelo e as premissas, discutiremos o conjunto de dados, SAMGODS.
Dados e justificativa - SAMGODS
Para analisar os efeitos potenciais do PI por meio da demanda derivada para distribuição, utilizamos a Suécia como um caso quantitativo. Como os países vizinhos possuem fluxos de carga semelhantes e respectivas diferenças no transporte norte-sul, incluir dados desses países não resultaria em diferenças quanto aos efeitos relativos do nível de compatibilidade dos contêineres PI. Todos os volumes nacionais carregados e descarregados na Suécia foram obtidos utilizando os dados SAMGODS (Vierth et al. 2012; Bergquist et al. 2016; Karlsson e Bernhardsson 2018), cortesia da Administração de Tráfego Sueca. Trata-se de uma matriz origem–destino de todos os fluxos domésticos de carga na Suécia, com o município como origem–destino. Os dados do SAMGODS foram utilizados em numerosos estudos na última década (por exemplo, Ljungberg 2013; Pålsson et al. 2017; Pålsson e Sternberg 2018; Jensen et al. 2019), e Karlsson e Bernhardsson (2018) explicaram sua calibração. Localizada no canto da Europa, a Suécia oferece acesso a dados de carga de alta qualidade, possui longas distâncias de transporte e tem recebido muita atenção de pesquisa; portanto, a Suécia é adequada para análise do PI.
Os dados SAMGODS dividem a carga em 35 categorias, baseadas em suas características (por exemplo, paletizada, tanque, carga seca a granel) e tipo de veículo requerido (por exemplo, trailer refrigerado, veículo para madeira). Para calcular os efeitos da Internet Física nos balanços de carga na Suécia, focamos nas 12 categorias de carga dos dados SAMGODS que são transportadas nas mesmas combinações de veículos que a carga geral.
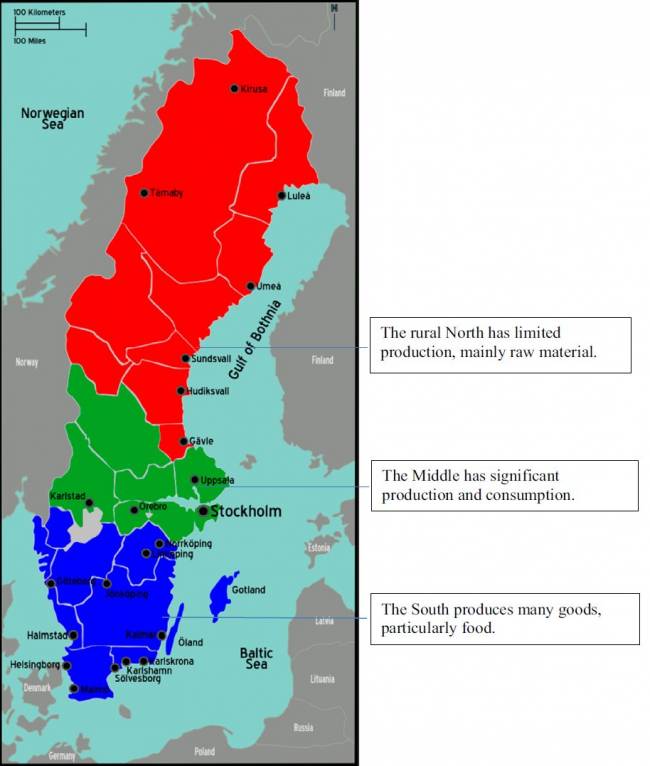
As 12 categorias foram selecionadas em colaboração com especialistas da indústria e após inspeções visuais dos fluxos norte-sul e sul-norte. Usamos as três regiões geográficas da Suécia como representação dos fluxos de carga intra-regionais (ver Figura 3). Essas regiões representam uma diversidade significativa em termos de oferta e demanda de bens. A Figura 3 fornece uma visão simplificada da oferta e demanda regional de bens da Suécia.
Em termos de modularidade, a compatibilidade entre diferentes transportes de contêineres PI determina se a Internet Física diminuirá a modularidade (conforme descrito na seção anterior). Implementações futuras da Internet Física podem incluir contêineres PI adotados para cargas a granel, o que significa que o PI poderia possivelmente aumentar a modularidade. No entanto, tais implementações são mais prováveis de ocorrer após a realização de uma massa crítica de hubs PI e operadores participantes.
Contribuições dos especialistas às suposições
A qualidade de qualquer modelo depende das suposições subjacentes (Waller e Fawcett 2012); assim, consultamos seis especialistas em distribuição física entre 2012 e 2018 (Tabela 1). Esses especialistas foram selecionados com base em sua competência e experiência na logística do mundo real, com foco específico em operações terminal-a-terminal em operações suecas de âmbito nacional.
Tradicionalmente, modelos matemáticos são validados por dados do mundo real. Como não existe uma Internet Física real, não há dados do mundo real para validar o modelo, aumentando a importância do uso de dados de entrada confiáveis e suposições apropriadas ao analisar a Internet Física.
O MODELO
Com base em nossa pergunta de pesquisa e nos dados do SAMGODS, formulamos um modelo matemático que imita a Internet Física. O modelo tem como objetivo minimizar os desequilíbrios nos fluxos de contêineres PI entre os hubs PI. Como discutido anteriormente, os desequilíbrios de fluxo podem ser devidos a desequilíbrios comerciais entre as regiões ou diferentes tipos de frete que necessitam de diferentes tipos de contêineres PI. Assumimos que a quantidade (em toneladas) e os tipos de frete que um hub deve fornecer a outros hubs indicam sua demanda pela quantidade (em toneladas) e tipos de contêineres PI. Da mesma forma, a quantidade (em toneladas) e os tipos de frete que um hub deve receber de outros hubs indicam sua oferta pela quantidade (em toneladas) e os tipos de contêineres PI.
Uma vez que as características (tamanho e peso) do contêiner PI usado para uma categoria específica de frete são conhecidas, o número de contêineres PI desse tipo (com base no tamanho) pode ser calculado para a quantidade a ser transportada nesse tipo/tamanho de contêiner PI. Com base nos pressupostos da PI, assumimos que os contêineres PI são roteados automaticamente por diferentes rotas de suas origens aos destinos (nosso foco sendo o transporte terminal a terminal). O objetivo é movimentar contêineres PI entre terminais minimizando os fluxos reversos, ou seja, o reposicionamento de contêineres PI vazios. Nosso modelo é aplicável ao transporte inter-regional em uma Internet Física e não depende se a primeira e a última milha até o respectivo hub regional de PI são realizadas na PI ou por meio de transporte convencional (Fazili et al. 2017).
| Especialista # | Dados | Observações e notas especiais | Contribuição para suposições |
|---|---|---|---|
| 1. Consultor sênior de transporte macro | Duas entrevistas e vários e-mails 2016–2017 | O consultor sênior macro auxiliou os pesquisadores na proposição de tipos compatíveis de frete e na realização de agregações corretas dos dados SAMGODS. O consultor revisou uma versão anterior deste artigo. | #3 & 6 |
| 2. Gerente distrital (prestador internacional de serviços logísticos) | Entrevista por telefone 2012 | O gerente distrital explicou a colaboração horizontal e vertical entre os prestadores de serviços logísticos e os clientes na zona rural do Norte da Suécia. | #2 |
| 3. CEO e 4. Chefe de Relações com Membros (Associação de Transportadoras) |
Diversas reuniões presenciais e por telefone 2016–2018 | A associação de transportadoras representa mais de 100 empresas rodoviárias que operam o transporte de longa distância e a distribuição para um grande prestador de serviços logísticos. O CEO e o chefe de Relações com Membros forneceram contribuições valiosas sobre como suas empresas associadas operam suas linhas no sistema de centro e raios do prestador de serviços logísticos. | #2, 3, & 7 |
| 5. Gerente de operações de transportadora rodoviária que opera um terminal | Duas entrevistas por telefone e vários e-mails 2017 | O gerente de operações desta transportadora rodoviária no Norte da Suécia gerencia um centro e supervisiona o carregamento de mercadorias em direção ao sul e o descarregamento de mercadorias em direção ao norte. Por mais de duas semanas, o gerente de operações tirou fotografias sistemáticas do carregamento de todos os caminhões que chegavam e partiam. | #2, 3, & 6 |
| 6. Motorista (grande prestador nacional de serviços logísticos) | Diversas discussões informais 2017 | Um motorista empregado por um grande prestador nacional de serviços logísticos tirou, com permissão, fotos de todos os caminhões que saíam do terminal de Gotemburgo. Esse motorista tem mais de 20 anos de experiência com todos os tipos de veículos e esteve envolvido em inúmeros projetos de pesquisa e desenvolvimento sobre eficiência de motoristas. Ele foi informado sobre a Internet Física; ajudou como parceiro de discussão; e forneceu contribuições sobre taxas de ocupação, embalagens e suposições de peso. | #3 |
O modelo é geral o suficiente para lidar com qualquer número de nós na rede interconectada de PI-hubs e qualquer número de tipos de carga. Um aspecto importante que queremos analisar é a compatibilidade do fluxo de PI-contêineres com a carga real. Para esse propósito, nosso modelo trata de quatro cenários de compatibilidade, conforme detalhado abaixo, onde K indica o número de tipos de carga, e C indica o número de grupos de PI-contêineres compatíveis.
• Com compatibilidade total, que é o melhor caso, todos os tipos de carga podem ser combinados de modo que haja apenas um (C = 1) tipo de PI-contêiner que precise ser contado.
• Sem compatibilidade, que é o pior caso, cada tipo de carga deve ser transportado separadamente em C = K diferentes tipos de PI-contêineres.
• Com compatibilidade limitada, que está mais próximo do caso sem compatibilidade, a carga deve ser transportada em C = 2K/3 diferentes tipos de PI-contêineres.
• Com alguma compatibilidade, mais próximo do caso de compatibilidade total, a carga deve ser transportada em C = K/3 diferentes tipos de PI-contêineres.
Fornecemos modelos para cada um dos quatro casos explicados acima. Os modelos permanecem os mesmos, exceto pelo valor de C (o número de grupos de compatibilidade) e os tipos de carga em cada grupo de compatibilidade. Após alcançar o hub principal em uma região, os fluxos dentro dessa região estão fora do escopo estratégico do nosso modelo. Primeiro, definimos as notações usadas no modelo de balanceamento de fluxo:
Conjuntos
$$ H = \{1, \dots, N\}, \text{ conjunto de todos os hubs.} $$
$$ F = \{1, \dots, K\}, \text{ conjunto de todos os tipos de carga.} $$
$$ F^p \subset F = \text{ subconjunto } p \text{ dos tipos de carga que são compatíveis em termos de PI-contêineres } p = 1, \dots, C $$
Índices
$$ i, j \in H \text{ indicam hubs regionais.} $$
$$ k \in F \text{ indica tipo de carga ou PI-contêiner.} $$
$$ p = 1, \dots, C \text{ indica um grupo de tipos de cargas compatíveis.} $$
Parâmetros
$$ D_{jkp} \text{:} \text{ demanda em toneladas para PI-contêineres no hub } j \text{ para o tipo de carga } k \in F^p \text{ para } p = 1, \dots, C $$
$$ S_{ikp} \text{:} \text{ oferta em toneladas para PI-contêineres no hub } i \text{ para o tipo de carga } k \in F^p \text{ para } p = 1, \dots, C $$
Variáveis de decisão
$$ X_{pij} \text{:} \text{ o fluxo em toneladas da carga do hub } i \text{ para } j \text{ para } p = 1, \dots, C \text{ (total para todo } k \in F^p\text{)} $$
$$ fb_{pij} \text{:} \text{ a diferença em toneladas entre os fluxos entre o hub } i \text{ para } j \text{ e o hub } j \text{ para } i \text{ para } p = 1, \dots, C \text{ (total para todo } k \in F^p\text{)} $$
A Figura 4 representa o modelo de rede PIC. No Modelo PIC, C ∈ {1, 4, 8, 12} indica a compatibilidade assumida. Nesse sentido, temos quatro modelos equivalentes.
Modelo PIC
$$ \text{Min } \sum_{p=1}^{C} \sum_{i=1}^{N} \sum_{j=i+1}^{N} |fb_{pij}| \quad (1) $$
Sujeito a.
$$ \sum_{j=1}^{N} X_{pij} \leq \sum_{k \in F^p} S_{ikp} \text{ para todos } i \text{ e } p \in \{1, \dots, C\} \quad (2) $$
$$ \sum_{i=1}^{N} X_{pij} = \sum_{k \in F^p} D_{jkp} \text{ para todos } j \text{ e } p \in \{1, \dots, C\} \quad (3) $$
$$ fb_{pij} = X_{pij} - X_{pji} \text{ para todos } p \in \{1, \dots, C\}, i \in H, \text{ e } j = i+1, \dots, N \quad (4) $$
$$ X_{kij} \geq 0 \text{ para todos } k \in F^C \text{ e } i, j \in H \quad (5) $$
$$ fb_{kij} \text{ irrestrito } k \in F^C \text{ e } i, j \in H \quad (6) $$
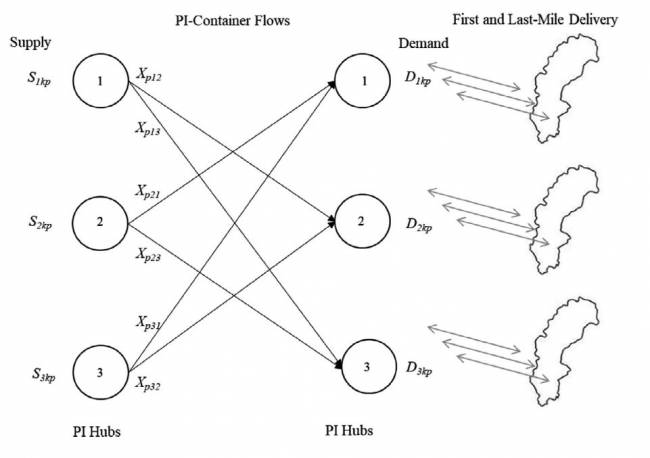
A função objetivo (1) do Modelo PIC calcula os desequilíbrios totais de fluxo entre os hubs de origem e destino. Deve-se notar que a função inclui uma função valor absoluto tornando o modelo não linear. Posteriormente, linearizamos essa função adicionando novas variáveis e restrições ao modelo (Apêndice A). No conjunto de restrições (2), garantimos que os contêineres PI que vão do hub j para os outros hubs não excedam o número recebido no hub j (veja a Figura 4). No conjunto de restrições (3), garantimos que o hub i receba todos os contêineres PI que necessita (veja a Figura 4). Nos conjuntos de restrições (2) e (3), consideramos cada grupo de compatibilidade, p, como uma mercadoria agregada, calculando assim o fornecimento total e a demanda total para o grupo p somando o fornecimento e a demanda das mercadorias desse grupo. O valor máximo de p vem de C, indicando quantos grupos de compatibilidade existem em cada cenário. No conjunto de restrições (4), calculamos os desequilíbrios de fluxo para cada grupo de compatibilidade p entre cada hub.
Os contêineres PI devem ser reposicionados; portanto, devemos calcular os desequilíbrios em apenas uma direção, pois eles serão os mesmos na direção reversa. O conjunto de restrições (5) garante a não negatividade dos fluxos, e o conjunto de restrições (6) especifica que os desequilíbrios são irrestritos em sinal.
Para resolver o modelo como um programa linear, a função objetivo deve ser linearizada adicionando um novo conjunto de variáveis e restrições aos modelos, conforme detalhado no Apêndice A.
Suposições
Esta seção discute as suposições subjacentes do nosso artigo.
Suposição #1: Rede logística híbrida
Dado o enorme investimento e o tempo necessário para construir os componentes da Internet Física, décadas de sistemas híbridos estão no futuro. Fazili et al. (2017) descrevem um sistema híbrido, isto é, o sistema logístico convencional coexistindo com a Internet Física. Portanto, a suposição de um sistema híbrido é a mais realista e a aplicada neste artigo. A implementação de tal rede logística híbrida supõe que a fronteira entre os sistemas logísticos convencional e PI pode ser o hub PI; isto é, bens podem ser descarregados no hub PI e embalados nos contêineres PI do hub. Dado seu contexto estratégico (Bartolacci et al. 2012), este manuscrito descreve o "PI" do sistema (transporte intra-regional terminal a terminal).
Suposição #2: Taxa de ocupação de caminhões em rotas desequilibradas
Com suas longas distâncias, cidades rurais e aldeias, o norte da Suécia é caracterizado por uma colaboração horizontal significativa (descrita, por exemplo, por Hagebäck e Segerstedt (2004)). Os dois maiores varejistas de alimentos, ICA e COOP, distribuem conjuntamente para os varejistas de alimentos; e os provedores de serviços logísticos Schenker e DHL colaboram. Essa colaboração é impulsionada pela necessidade absoluta de maximizar as taxas de preenchimento, conforme verificado em uma entrevista com um gerente regional do norte (Especialista 2). Embora não seja tão fortemente aplicada, as rotas para áreas com alta demanda por mercadorias (por exemplo, Estocolmo) estão praticamente cheias. Assim, os transportadores rodoviários sabem que é muito improvável conseguirem uma carga de retorno e terão que voltar vazios (Especialistas 3, 4 e 5).
Suposição #3: Peso e dobrabilidade da embalagem
Carga geral geralmente não são bens paletizados, mas sim material de construção e componentes, tambores, barris, componentes de veículos, etc., que representam todos os fluxos de carga entre origem e destino—normalmente com diferentes tipos de carga indo nas respectivas direções (Especialistas 1 e 5 e conjunto de dados de frete). Assumimos, para fins do nosso modelo, que o peso da embalagem (e capacidade) da caixa média m (400 × 600 × 400) representa todos os tipos de contêineres PI menores ou maiores (ou caixas m e versões especializadas futuras das caixas m). Essa suposição não será verdadeira, já que contêineres PI específicos projetados para um ou mais tipos de mercadorias terão tamanho diferente da caixa m; contudo, isso não afetará significativamente os resultados (que analisam o efeito agregado da rede). Segundo Landschützer et al. (2018), uma caixa m regular pesa 4,5 kg. A caixa m é projetada em relação à Euro-pallet (base de 800 mm × 1200 mm); ou seja, 4 caixas m podem ser carregadas por pallet (base) e empilhadas em 6 alturas. Considerando que uma combinação sueca regular tem 18 pallets no caminhão + 33 no trailer, o peso da embalagem é 51 × 4 × 6 × 4,5 kg = 5508 kg (1224 contêineres PI (caixas m) * 4,5 kg). No transporte de carga geral na Suécia, a restrição de volume da combinação veicular é tipicamente o fator limitante em vez do limite de peso[2]. Um caminhão cheio pesa 25 toneladas e pode acomodar 1224 caixas m. Portanto, assume-se que um contêiner PI representativo carrega 20,42 kg. Embora as caixas m atualmente não sejam dobráveis, presumimos que serão em versões futuras (nos cenários de fluxos compatíveis); caso contrário, todo a Internet Física se torna um sistema de via única com contêineres PI cheios na ida e vazios na volta (especificidade de sinergia conforme explicado no quadro baseado na modularidade do serviço).
Suposição #4: Desequilíbrios agregados
Até onde sabemos, os desequilíbrios de fluxo entre origem e destinos não foram abordados no contexto PI (Sternberg e Norrman 2017). Em contraste, nosso modelo aborda essa questão em nível agregado. Não incluímos quaisquer restrições operacionais (por exemplo, janelas de tempo, tempos de entrega, carregamento e descarregamento), que são críticas para o planejamento operacional no PI; contudo, elas são desnecessárias para determinar os efeitos dos desequilíbrios. Nosso propósito não é fornecer uma solução detalhada para um problema operacional do PI (cf. Hauder et al. 2018), mas estudar como desequilíbrios comerciais e (in)compatibilidade de cargas podem gerar a necessidade de reposicionamento vazio de contêineres PI.
Suposição #5: Economia da diversidade de produtos
Uma suposição subjacente é que a heterogeneidade das demandas por serviços de logística e transporte permanecerá constante; ou seja, os clientes continuarão consumindo uma grande variedade de bens, isto é, economia da diversidade de produtos (Suzuki e Lu 2017). Considerando essas questões, as taxas de preenchimento fornecidas por Wall (2013) e Pålsson e Sternberg (2018), e o peso dos PI-containers, utilizamos 25 toneladas como o peso quando a capacidade máxima de volume de uma combinação de caminhão é utilizada (como explicado anteriormente, o volume e não o peso determina quando um caminhão que transporta carga geral está cheio).
Suposição #6: Compatibilidade dos PI-containers (categorias de cargas)
As 12 categorias de cargas identificadas (SAMGODS) atualmente são transportadas usando o mesmo caminhão e sem embalagens de transporte designadas (além dos Euro-paletes). Para ilustrar isso no contexto de diferentes tipos de cargas indo em direções diferentes, veja a Figura 5.

Com base em consultas com especialistas (particularmente com o Especialista 1), nossa matriz de compatibilidade assume as seguintes propriedades:
Compatibilidade total (Cenário 1): Este caso existe atualmente; ou seja, diferentes tipos de carga geral podem ser transportados em duas direções (carga circulando entre dois hubs) usando o mesmo veículo (Especialista 5). Isso é ilustrado na Figura 6.
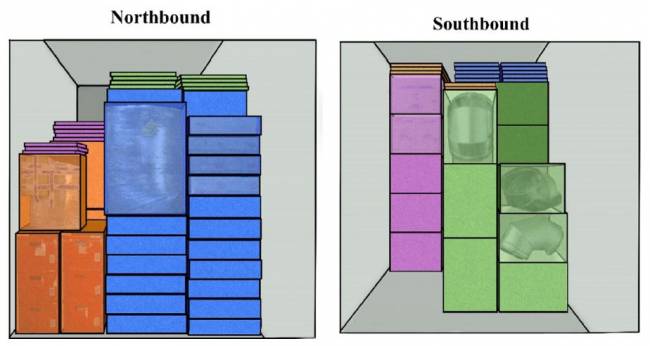
Sem compatibilidade (Cenário 2): PI-contêineres altamente especializados impedem a integração entre as remessas, pois um efeito dos PI-contêineres é serem altamente específicos para cada tipo de carga (ilustrado na Figura 7).
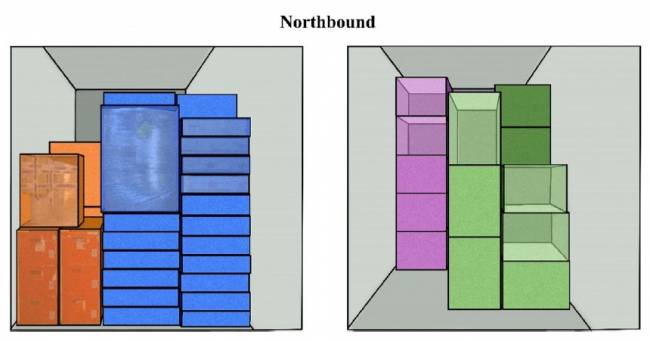
Compatibilidade limitada (Cenário 3): Neste caso, assumimos que alguns dos tipos de carga mais similares e fáceis de carregar são compatíveis, enquanto os outros não são, resultando na seguinte matriz:
Nas Figuras 8 e 9, ilustramos compatibilidade limitada; ou seja, mais, mas não todos os tipos de carga podem usar os mesmos PI-contêineres. Subsequentemente, este cenário levará a mais reposicionamentos do que no Cenário 1 (compatibilidade total), mas significativamente menos do que no Cenário 2 (sem compatibilidade).
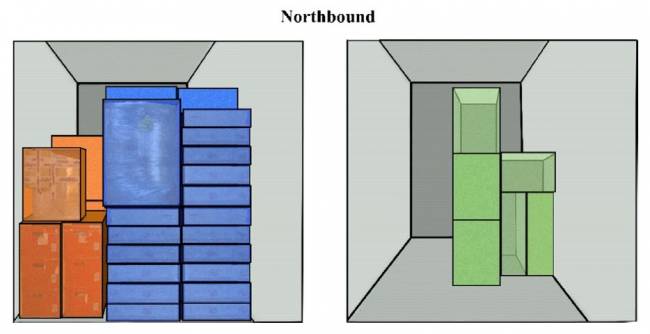
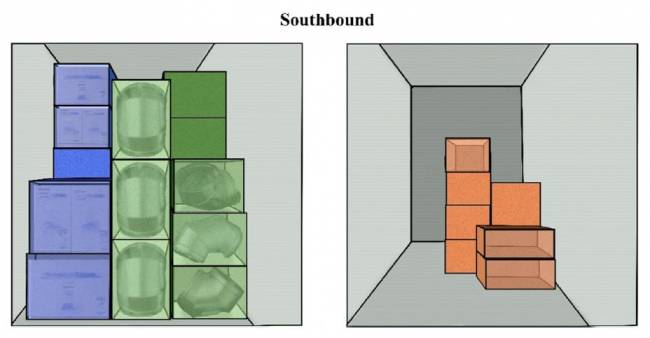
Alguma compatibilidade (Cenário 4): Neste caso, alimentos, têxteis e ração podem ir juntos; e madeira, metal e papel são compatíveis, resultando no seguinte:
Suposição #7: PI utiliza controle centralizado; o sistema convencional não utiliza
O Cenário 1 representa a otimização dos fluxos em um cenário de contêineres PI totalmente compatíveis. Teoricamente, esse cenário poderia ser aplicado ao controle centralizado de todos os fluxos em uma rede logística convencional (ou seja, agrupamento tradicional de recursos sem implementar o PI). No entanto, Simmer et al. (2017), por exemplo, observam que os atores relutam em abrir mão do controle. Portanto, o controle centralizado em um sistema logístico convencional é considerado irrealista (a menos que o ambiente crie urgência para isso, como em Hagebäck e Segerstedt (2004)). Os especialistas 3 e 4 também enfatizaram fortemente esse ponto. Portanto, este manuscrito foca apenas em cenários com PI implementado.
RESULTADOS
Nesta seção, apresentamos os resultados dos modelos utilizando dados de transporte interregional de cargas das diversas regiões norte, centro e sul da Suécia. Nosso conjunto de dados contém 12 tipos de carga transportados entre três regiões principais (hubs).
A Figura 10 apresenta os resultados dos desequilíbrios totais para todos os cenários de compatibilidade comparados entre si.
Como observado na Figura 10, a compatibilidade faz uma diferença significativa nos desequilíbrios totais de fluxo. Na prática atual, a carga é transportada em pallets que podem ser carregados no mesmo contêiner. Os desequilíbrios são os segundos menores (estado atual) entre todos os cenários, provavelmente porque não há otimização centralizada. O valor otimizado (C = 1) é menor que o caso como está. O maior desequilíbrio é observado quando os contêineres PI não são compatíveis, C = 12. Os Cenários 2 e 3 para C = 8 e C = 4, respectivamente, seguem um padrão decrescente conforme a compatibilidade aumenta.
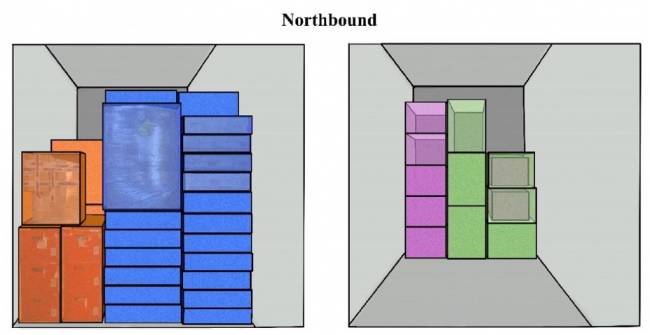
No gráfico à direita da Figura 10, os desequilíbrios estão distribuídos entre as regiões. O desequilíbrio entre as regiões sul e centro é o maior. O comércio entre essas duas regiões representa a maior parte no país. Curiosamente, a prática atual e os resultados do cenário ótimo (C = 1) estão invertidos, com a prática real apresentando menor desequilíbrio entre as regiões sul e centro, embora o cenário ótimo, C = 1, seja o menor em todas as regiões, como esperado. Lembre-se de que a otimização envolve todas as regiões. Os resultados para cada cenário de compatibilidade são os seguintes: C = 1 representa a modularidade de serviço inalterada; e C = 4, C = 8 e C = 12 representam modularidades decrescentes.
No modelo de PL, usamos toneladas como unidade de transporte e, portanto, a solução do modelo fornece os desequilíbrios entre diferentes regiões em toneladas. No entanto, pode haver interesse em saber quantos contêineres PI precisam ser reposicionados. Se o tamanho do contêiner PI (quanto peso de uma categoria de produto ele carrega), com base nos desequilíbrios em toneladas, for conhecido, o número de contêineres PI que precisam ser reposicionados pode ser calculado. Observe que cada grupo de compatibilidade pode estar diretamente associado a um tamanho diferente de contêiner PI. Isso não significa que diferentes tamanhos de contêineres PI não possam ser usados para o mesmo grupo de compatibilidade. Nesse caso, precisamos assumir um tamanho médio de contêiner PI se houver a necessidade de calcular o número de contêineres PI a serem reposicionados. Nosso modelo de PL assume as melhores taxas de preenchimento e não impõe restrição ao tamanho do contêiner PI. Se as taxas reais de preenchimento forem menores, a necessidade de reposicionamento de contêineres PI vazios será maior. No Apêndice C, apresentamos o número de contêineres PI a serem reposicionados em cada cenário com base nos desequilíbrios totais apresentados na Figura 10.
Cenário 1: C = 1
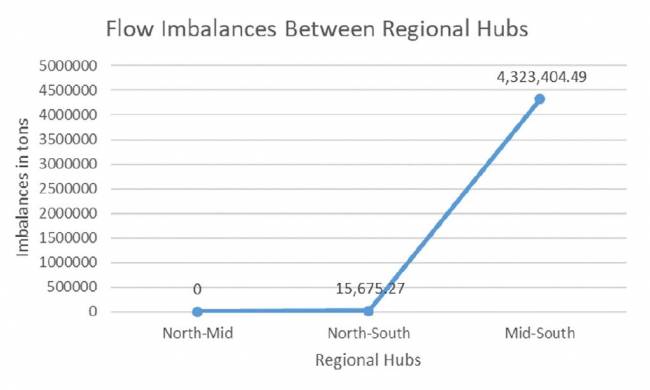
Quando C = 1, assumimos que os contêineres PI são universalmente compatíveis e intercambiáveis para todos os tipos de frete (como a carga geral de hoje). Abordando a Internet Física como Montreuil (2011) pretendia, esse cenário ideal pode agregar todos os fluxos ao calcular os desequilíbrios de fluxo. Nossos resultados com dados inter-regionais da Suécia indicam o desequilíbrio total minimizado de 4.339.079,76 toneladas de frete (veja a Figura 10), o que equivale a 173.564 viagens de caminhão, cada uma transportando 25 toneladas de frete líquido. Os desequilíbrios entre hubs regionais representam 7,6% da atividade total de transporte (de 57.157.318,12 toneladas); esses desequilíbrios são mostrados no Apêndice B, e uma representação gráfica é fornecida na Figura 11.
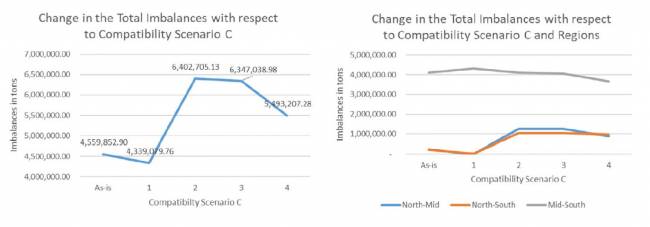
Uma comparação entre os desequilíbrios minimizados (4.339.079,76 toneladas ou 7,6%) e aqueles nos fluxos atuais (4.559.852,90 toneladas ou 8%, calculados usando os dados dos fluxos atuais) reflete o potencial de melhoria do uso da otimização para determinar os fluxos entre os PI-hubs.
Cenário 2: C = 12
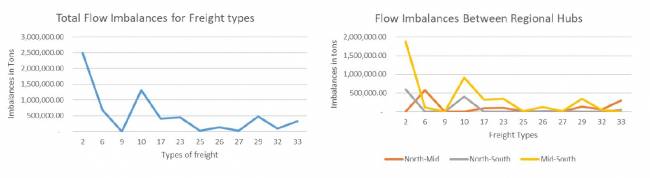
No Cenário 2, assumimos que não há compatibilidade entre as cargas em termos dos contêineres PI, o que significa que diferentes tipos de carga (veja a Tabela 2) não podem ser transportados nos mesmos contêineres PI e que o serviço logístico torna-se menos modularizado. Assim, é o pior cenário possível. Nossos resultados mostram que o desequilíbrio total do fluxo é de 6.402.705,13 toneladas (veja a Figura 10), equivalendo a 256.109 caminhões que podem transportar 25 toneladas. A carga total transportada é de 57.157.318,12 toneladas. Portanto, os desequilíbrios representam 11,2% da atividade total de transporte. Os desequilíbrios detalhados entre os hubs regionais são apresentados no Apêndice B, e uma representação gráfica é fornecida na Figura 12.
| Mercadoria (tipo) | Incluído neste estudo |
|---|---|
| 1 Cereais (granel seco) | |
| 2 Batatas, outros vegetais, frescos ou congelados, frutas frescas (granel seco) | X |
| 3 Animais vivos (granel seco) | |
| 4 Beterraba para açúcar (granel seco) | |
| 5 Madeira para a indústria de papel (madeira para polpa) (granel seco) | |
| 6 Madeira aproximadamente quadrada ou serrada longitudinalmente, fatiada ou descascada (granel seco) | X |
| 7 Cavacos de madeira e resíduos de madeira (granel seco) | |
| 8 Outra madeira ou cortiça (granel seco) | Sem matriz PWC |
| 9 Têxteis, artigos têxteis e fibras artificiais, outras matérias-primas animais e vegetais (carga geral) | X |
| 10 Alimentos e ração animal (carga geral) | X |
| 11 Sementes oleaginosas e frutos oleaginosos e gorduras (granel líquido) | |
| 12 Combustíveis minerais sólidos (granel líquido) | |
| 13 Petróleo bruto (granel líquido) | |
| 14 Produtos de petróleo (granel líquido) | |
| 15 Minério de ferro, resíduos de ferro e aço e pó de alto-forno (granel seco) | |
| 16 Minérios e resíduos não ferrosos (granel seco) | |
| 17 Produtos metálicos (carga geral) | X |
| 18 Cimento, cal, materiais de construção manufaturados (granel seco) | |
| 19 Terra, areia e cascalho (granel seco) | |
| 20 Outros minerais brutos e manufaturados (granel seco) | |
| 21 Fertilizantes naturais e químicos (granel seco) | |
| 22 Produtos químicos do carvão (granel líquido) | |
| 23 Produtos químicos, exceto produtos químicos do carvão e alcatrão (granel seco) | X |
| 24 Polpa de papel e papel usado (granel seco) | |
| 25 Equipamentos de transporte, montados ou não, e suas partes (carga geral) | X |
| 26 Manufaturados de metal (carga geral) | X |
| 27 Vidro, vidrarias, produtos cerâmicos (carga geral) | X |
| 28 Papel, papelão; não manufaturados (granel seco) | |
| 29 Couro têxtil, vestuário, outros artigos manufaturados que não sejam papel, papelão e seus manufaturados (carga geral) | X |
| 30 Cargas mistas e parciais, artigos diversos (carga geral) | Sem matriz PWC |
| 31 Madeira para serraria (granel seco) | |
| 32 Máquinas, aparelhos, motores, montados ou não, e suas partes (carga geral) | X |
| 33 Papel, papelão e seus manufaturados (carga geral) | X |
| 34 Material para embalagens, usado (granel seco) | Sem matriz PWC |
| 35 Carga aérea (carga geral) |
Cenário 3: C = 8
No Cenário 3, estamos assumindo compatibilidade parcial entre os tipos de frete mostrados na Tabela 3. Temos oito grupos de frete; os tipos de frete em cada grupo são compatíveis entre si e podem compartilhar os mesmos contêineres PI. Nossos resultados mostram que o desequilíbrio total de fluxo é de 6.347.038,98 toneladas (veja a Figura 10), o que equivale a 253.882 caminhões com capacidade para 25 toneladas. O total de frete transportado é de 57.157.318,12 toneladas. Portanto, os desequilíbrios representam 11,1% da atividade total de transporte, não sendo significativamente diferente do Cenário 2. Reduzir para 8 grupos compatíveis a partir de 12 (cenário sem compatibilidade) não teve grande impacto. Os desequilíbrios detalhados entre os centros regionais estão mostrados no Apêndice B, e uma representação gráfica é fornecida na Figura 13.
| Categorias | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Tipos de frete | 2, 10 | 9, 29 | 6 | 17 | 23 | 25, 26 | 27, 32 | 33 |
Cenário 4: C = 4
No Cenário 4, assumimos que existem mais tipos de carga compatíveis do que no Cenário 3. Com base na agrupamento da Tabela 4, temos quatro grupos de carga de forma que os tipos em cada grupo são compatíveis entre si e podem compartilhar os mesmos contêineres PI. Neste caso, os desequilíbrios totais são de 5.493.207,28 toneladas (ver Figura 10) e 219.728 caminhões de 25 toneladas. Esses desequilíbrios representam 10% da carga total. À medida que a carga se torna cada vez mais compatível com o contêiner PI, os desequilíbrios diminuem. No entanto, o mínimo no Cenário 1 corresponde a 7,6% de todo o transporte de carga na Suécia, sugerindo assim que os desequilíbrios entre as regiões em termos de oferta e demanda para diferentes tipos de mercadorias ainda exigirão fluxos reversos de contêineres vazios, correspondendo a 7,6% da atividade logística total nas rodovias. Os desequilíbrios detalhados entre os hubs regionais são mostrados no Apêndice B, e uma representação gráfica é fornecida na Figura 14.
| Categorias | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Tipos de carga | 2, 9, 10, 29 | 6, 17, 26, 33 | 23 | 25, 27, 32 |
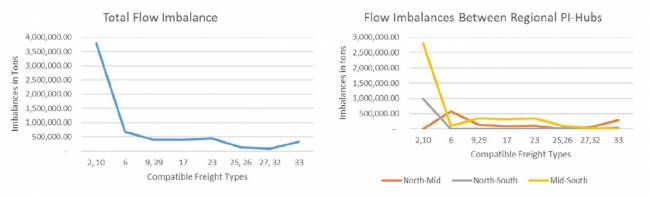
Como mostrado nas Figuras 13-15, os maiores desequilíbrios são para os tipos de carga ou grupos de compatibilidade que incluem os itens alimentícios 2 e 10. Novamente, os maiores desequilíbrios ocorrem entre as regiões sul e central (Figura 15).
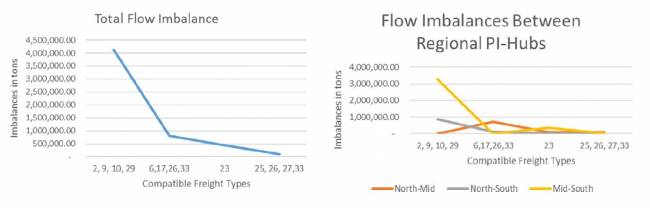
Para determinar se as mudanças nos dados de entrada afetam os resultados, também realizamos uma análise de sensibilidade considerando as seguintes modificações na demanda para diferentes cargas e regiões:
• A demanda nos três hubs (sul, centro e norte) foi reduzida em 10%, 7,5% e 5%, respectivamente (considerando a sensibilidade geral do modelo).
• Não houve redução para os tipos de frete 2 e 10 (alimentos), redução de 10% em todos os outros tipos.
• A demanda nos três hubs (sul, centro e norte) foi aumentada em 10%, 7,5% e 5%, respectivamente (considerando a sensibilidade geral do modelo).
Os dados originais foram obtidos em condições econômicas regulares. Assumimos que a demanda pode aumentar (boom econômico) ou diminuir (recessão econômica). Assim, consideramos primeiro o caso em que a demanda diminui em todas as regiões em certas proporções com base nos bens demandados nessas regiões. Em segundo lugar, assumindo que a demanda por itens alimentares permanece a mesma mesmo durante uma recessão, consideramos reduções na demanda para todos os itens, exceto alimentos. Em terceiro lugar, consideramos o caso em que a demanda aumenta devido a um boom econômico. Por questões de espaço, os resultados dessas suposições podem ser encontrados no Apêndice D.
IMPLICAÇÕES E DISCUSSÃO
Atendendo a vários chamados para pesquisa, este estudo analisou a Internet Física usando dados empíricos e suposições realistas baseadas em informações da literatura e de especialistas da indústria. Focamos em analisar os efeitos potenciais de diferentes níveis de heterogeneidade das entradas, determinados pela compatibilidade dos contêineres PI. Nossa análise revela um desequilíbrio no melhor cenário de 7,6%, o que representa uma melhoria em comparação com os desequilíbrios do sistema logístico convencional atual. Se a compatibilidade de embalagem entre os contêineres PI puder ser mantida (como no Cenário 1) e se os benefícios da automação em terminais habilitados pelos contêineres PI puderem ser aproveitados, a especificidade sinérgica será baixa. Além disso, a urgência dos principais stakeholders em promover a modularização por meio da Internet Física aumentará, porque o PI será um dos habilitadores da tecnologia, operacionalizando a otimização. No melhor cenário (Cenário 1), o PI representa uma visão desejável das cadeias de suprimentos futuras.
O desequilíbrio do melhor cenário (7,6%) deve ser comparado com os desequilíbrios de 11,2% e 11,1% nos cenários em que os contêineres PI não possuem compatibilidade (Cenários 2 e 3, respectivamente). A falta de compatibilidade entre os contêineres PI causará especificidade sinérgica contra a modularização e implementação da Internet Física, porque o conceito poderá falhar em melhorar as taxas de preenchimento. Em comparação com o Cenário 1, o Cenário 2 representa 82.545 cargas adicionais de caminhão por ano entre as regiões norte e sul, representando um custo extra substancial para os embarcadores e um impacto ambiental logístico negativo aumentado. Interessantemente, os Cenários 2 e 3 apresentam pouca diferença em termos do efeito sobre o volume total de frete. No entanto, à medida que a heterogeneidade relativa das entradas diminui no Cenário 4, o desequilíbrio total diminui para 10%.
Crítica e pesquisa futura
Nossa análise foi baseada em sete suposições, incluindo que as demandas heterogêneas dos serviços logísticos permanecerão constantes. Entretanto, recomenda-se que pesquisas futuras avaliem a validade dessa suposição, bem como das demais, por meio de testes-piloto da Internet Física, múltiplos estudos de caso ou pesquisas baseadas em questionários.
O modelo matemático que apresentamos neste artigo aborda o problema de reposicionamento de contêineres PI em nível estratégico e agregado entre os PI-hubs. Devido à sua natureza estratégica, este artigo não incorpora os detalhes operacionais do problema (por exemplo, como os contêineres PI são carregados com mercadorias para minimizar o número de contêineres PI necessários, como os contêineres de transporte são carregados com os contêineres PI, o tempo para carregar/descarregar os contêineres PI nos contêineres de transporte e os contêineres de transporte nos caminhões, e como os caminhões são roteirizados entre os PI-hubs). Incluir esses detalhes permitiria que o modelo fornecesse soluções para outros problemas operacionais no PI. Os modelos disponíveis na literatura tradicional de reposicionamento de contêineres marítimos podem servir de base para o desenvolvimento de modelos que incorporem as novas características do reposicionamento de contêineres PI. Tais modelos não serão apenas grandes devido à introdução de novas variáveis e restrições para abordar os detalhes mencionados anteriormente, mas também mais difíceis de resolver, especialmente quando envolvem variáveis inteiras/binárias típicas nesse tipo de modelagem. Esses fatores enfatizarão a necessidade de desenvolver procedimentos de solução eficientes que possam resolver tais modelos destinados ao planejamento central do PI diariamente. Tais modelos poderiam potencialmente incluir problemas de primeira e última milha e a relação com a logística colaborativa (Carbone et al. 2017; Castillo et al. 2018). Chen e Pan (2015) e Rai et al. (2017) sugeriram investigar o PI como uma forma de gerenciar a logística colaborativa.
Este artigo ilustra a importância da contínua pesquisa sobre contêineres PI, levando em consideração a teoria da modularidade e a heterogeneidade dos insumos. Projetos de pesquisa futuros devem intensificar os esforços de design para os contêineres PI se a Internet Física quiser manter sua posição como uma visão sustentável da logística do futuro. Propomos uma pesquisa interdisciplinar de ciência do design para abordar essa lacuna urgente em pesquisa e desenvolvimento. Além disso, tais esforços de pesquisa devem abordar a compatibilidade entre continentes, pois um sistema logístico projetado apenas para o mercado europeu poderia aumentar as ineficiências no transporte internacional. Dada a importância do sistema de embalagens, são necessárias pesquisas sobre como um sistema de embalagens em toda a indústria poderia ser adotado (por exemplo, estudando os sistemas secundários de embalagens adotados em toda a Escandinávia).
Implicações teóricas
Este artigo contribui para a teoria de alcance médio da modularização contextualizada de serviços logísticos (de Blok et al. 2014; Brax et al. 2017) ao analisar os efeitos estratégicos da modularização na Internet Física. Também contribui para a literatura crescente sobre a Internet Física ao mostrar a aplicabilidade e utilidade da operacionalização da teoria da modularidade aplicada aos serviços logísticos. Com base na modelagem matemática e na teoria da modularidade, nossos achados enfatizam a importância da modularização dos serviços logísticos sem aumentar a heterogeneidade dos insumos.
A pesquisa sobre a Internet Física ainda está em seus estágios iniciais, e muito trabalho permanece a ser feito. Nossa análise, assim como as direções de pesquisa futuras que oferecemos, destaca a importância de considerar o design da embalagem na modularização da logística e do transporte, e ainda mais no contexto da Internet Física.
Os resultados mostram que, se os componentes forem bem projetados, a Internet Física pode potencialmente reduzir desequilíbrios por meio da otimização dos fluxos de carga e do reposicionamento de contêineres PI. No entanto, também pode aumentar os desequilíbrios. A PI é essencialmente modularização, mas paradoxalmente pode resultar em menos compatibilidade dos serviços logísticos se os contêineres PI não forem bem projetados. Esse paradoxo deve ser considerado em pesquisas futuras sobre os efeitos da Internet Física.
Implicações práticas
Para que a Internet Física se torne uma realidade, serão necessários enormes investimentos tanto do setor público quanto do privado. Nosso modelo apresenta uma ferramenta valiosa para os formuladores de políticas na avaliação dos benefícios da implementação da PI. Além disso, fazemos uma contribuição significativa ao orientar as agências financiadoras sobre tópicos da PI que são vitalmente importantes para a implementação futura.
Os formuladores de políticas são lembrados de seu papel em criar a urgência necessária para promover a modularização. Recomenda-se à Comissão Europeia que pressionar por políticas que diminuem a urgência de modularizar (promovendo estratégias que facilitam o uso extensivo de transportadoras de baixo custo) e simultaneamente investir na implementação da Internet Física provavelmente não produzirá os efeitos desejados, semelhante a como a produção de baixo custo impediu a modularização da manufatura em grande escala (Starr 2010).
Usando nossos insights da pesquisa, os profissionais deverão ser capazes de ter uma visão objetiva dos potenciais efeitos dos contêineres PI em sua cadeia de suprimentos. Conforme exemplificado em nossas análises, a adoção de contêineres PI pode ter impacto positivo ou negativo nos equilíbrios de carga, dependendo do design do contêiner PI.
A PI representa ganhos significativos de eficiência, mas qualquer novo sistema de embalagem envolve um compromisso para os gestores. A adoção de embalagens que possibilitem automação pode ser benéfica, a menos que os ganhos sejam compensados pelo reposicionamento custoso da embalagem. Recomenda-se que os gestores acompanhem de perto o desenvolvimento da PI e, especificamente, a compatibilidade do sistema proposto de contêineres PI devido ao seu efeito na eficiência.
[1] ALICE é o acrônimo para Alliance for Logistics Innovation through Collaboration in Europe, uma organização de lobby formada para desenvolver uma estratégia para pesquisa, inovação e implantação de mercado da inovação em gestão da cadeia de suprimentos europeia. Entre os membros estão grandes corporações como Ford, Proctor & Gamble, Daimler e Volvo; partes interessadas públicas como o Correio Nacional Italiano e o Porto de Barcelona; e inúmeros institutos de pesquisa, como Mines ParisTech, Fraunhofer e RISE (https://www.etp-logistics.eu/?page_id=29).
[2] Isso está de acordo com os Especialistas 3, 4, 5 e 6, bem como em numerosos estudos sobre pesos médios (Wall 2013). A exceção (quando o peso é a restrição em vez do volume) geralmente são as matérias-primas (Pålsson e Sternberg 2018).
APÊNDICE A
LINEARIZAÇÃO DO MODELO PIC
Para linearizar a função objetivo no Modelo PI, definimos as seguintes variáveis técnicas e restrições.
Definimos um conjunto de variáveis técnicas como
$$ t_{pij} \text{ para todos } p \in \{1, \dots, C\}, i \in H, \text{ e } j = i+1, \dots, N $$
Adicionamos as seguintes restrições para substituir a restrição (4) no PI:
$$ t_{pij} \geq fb_{pij} \text{ para todos } p \in \{1, \dots, C\}, i \in H, \text{ e } j = i+1, \dots, N $$
$$ t_{pij} \geq -fb_{pij} \text{ para todos } p \in \{1, \dots, C\}, i \in H, \text{ e } j = i+1, \dots, N $$
Note que, como tpij são variáveis técnicas, não há definição em termos das características do problema. O modelo linearizado PIC-L pode então ser formulado como
PIC-L
$$ \text{Min } \sum_{p=1}^{C} \sum_{i=1}^{N} \sum_{j=i+1}^{N} t_{pij} $$
sujeito a
$$ \sum_{j=1}^{N} X_{pij} \leq \sum_{k \in F^p} S_{ikp} \text{ para todo } i \text{ e } p \in \{1, \dots, C\} $$
$$ \sum_{i=1}^{N} X_{pij} = \sum_{k \in F^p} D_{jkp} \text{ para todo } j \text{ e } p \in \{1, \dots, C\} $$
$$ t_{pij} \geq fb_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ e } j = i+1, \dots, N $$
$$ t_{pij} \geq -fb_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ e } j = i+1, \dots, N $$
$$ X_{kij} \geq 0 \text{ para todo } k \in F^C \text{ e } i, j \in H $$
$$ fb_{kij} \text{ irrestrito } k \in F^C \text{ e } i, j \in H $$
Note que usamos PIC-L em nossos experimentos.
APÊNDICE B
Este apêndice fornece os resultados com mais detalhes para os desequilíbrios totais de fluxo dos quatro cenários que simulamos usando nosso modelo matemático. Os números entre parênteses são os negativos do desequilíbrio na direção oposta. Por exemplo, na Tabela B1, o desequilíbrio entre norte e sul é 15.675,27, indicando que o norte envia esse tanto a mais de carga (em toneladas) para o sul. Portanto, o desequilíbrio entre sul e norte é 15.675,27, indicando que o sul envia esse tanto a menos de carga (em toneladas) para o norte.
Tabela B1: Desequilíbrios de fluxo entre hubs regionais na Suécia para o Cenário 1 C = 1
| De/Para | Norte | Meio | Sul |
|---|---|---|---|
| Norte | – | – | 15.675,27 |
| Meio | – | – | 4.323.404,49 |
| Sul | (15.675,27) | (4.323.404,49) | – |
Tabela B2: Desequilíbrios de fluxo entre centros regionais na Suécia para o Cenário 2 C = 12
94| Tipo de carga | De/Para | Norte | Centro | Sul |
|---|---|---|---|---|
| 2 | Norte | – | – | 593.224,25 |
| Centro | – | – | 1.887.794,49 | |
| Sul | (593.224,25) | (1.887.794,49) | – | |
| 6 | Norte | – | (577.627,15) | – |
| Centro | 577.627,15 | – | 106.659,86 | |
| Sul | – | (106.659,86) | – | |
| 9 | Norte | – | – | 15. |
| Meio | – | – | 5,06 | |
| Sul | (15,94) | (5,06) | – | |
| 10 | Norte | – | – | 396.501,19 |
| Meio | – | – | 914.356,22 | |
| Sul | (396.501,19) | (914.356,22) | – | |
| 17 | Norte | – | 84.064,81 | – |
| Meio | (84.064,81) | – | (317.317,87) | |
| Sul | – | 317.317,87 | – | |
| 23 | Norte | – | (99.093,37) | – |
| Meio | (99.093,37) | – | 345.368,23 | |
| Sul | – | (345.368,23) | – | |
| 25 | Norte | – | 12.148,84 | – |
| Central | (12.148,84) | – | (5.328,56) | |
| Sul | – | 5.328,56 | – | |
| 26 | Norte | – | – | 12.500,91 |
| Central | – | – | 125.393,69 | |
| Sul | (12.500,91) | (125.393,69) | – | |
| 27 | Norte | – | – | 9.248,68 |
| Central | – | – | 11.797,78 | |
| Sul | (9.248,68) | (11.797,78) | – | |
| 29 | Norte | – | (134.150,75) | – |
| Centro | 134.150,75 | – | 341.745,08 | |
| Sul | – | (341.745,08) | – | |
| 32 | Norte | – | 50.500,36 | – |
| Centro | (50.500,36) | – | (46.203,59) | |
| Sul | – | 46.203,59 | – | |
| 33 | Norte | – | (294.976,84) | (36.681,61) |
| Centro | 294.976,84 | – | – | |
| Sul | 36.681,61 | – | – | |
Tabela B3: Desequilíbrios de fluxo entre hubs regionais na Suécia para o Cenário 3 C = 8
| Tipo de frete | De/Para | Norte | Meio | Sul |
|---|---|---|---|---|
| 2, 10 | Norte | – | – | 989.725,44 |
| Meio | – | – | 2.802.150,71 | |
| Sul | (989.725,44) | (2.802.150,71) | – | |
| 6 | Norte | – | (577.627,15) | – |
| Meio | 577.627,15 | – | 106.659,86 | |
| Sul | – | (106.659,86) | – | |
| 9, 29 | Norte | – | (134.134,81) | – |
| Meio | 134.134,81 | – | 341.766,08 | |
| Sul | – | (341.766,08) | – | |
| 17 | Norte | – | 84.064,81 | – |
| Centro | (84.064,81) | – | (317.317,87) | |
| Sul | – | 317.317,87 | – | |
| 23 | Norte | – | (99.093,37) | – |
| Centro | 99.093,37 | – | 345.368,23 | |
| Sul | – | (345.368,23) | – | |
| 25, 26 | Norte | – | – | 24.649,75 |
| Centro | – | – | 107.916,28 | |
| Sul | (24.649,75) | (107.916,28) | – | |
| 27, 32 | Norte | – | 59.749,04 | – |
| Centro | (59.749,04) | – | (25.157,13) | |
| Sul | – | 25.157,13 | – | |
| 33 | Norte | – | (294.976,84) | (36.681,61) |
| Centro | 294.976,84 | – | – | |
| Sul | 36.681,61 | – | – | |
Tabela B4: Desequilíbrios de fluxo entre hubs regionais na Suécia para o Cenário 4 C = 4
| Tipo de carga | De/Para | Norte | Centro | Sul |
|---|---|---|---|---|
| 2, 9, 10, 29 | Norte | – | – | 855.590,63 |
| Centro | – | – | 3.278.051,60 | |
| Sul | (855.590,63) | (3.278.051,60) | – | |
| 6, 17, 26, 33 | Norte | – | (703.274,86) | (109.445,02) |
| Centro | 703.274,86 | – | – | |
| Sul | 109.445,02 | – | – | |
| 23 | Norte | – | (99.093,37) | – |
| Centro | 99.093,37 | – | 345.368,23 | |
| Sul | – | (345.368,23) | – | |
| 25, 27, 32 | Norte | – | – | 24.649,75 |
| Centro | – | – | 107.916,28 | |
| Sul | (24.649,75) | (107.916,28) | – | |
APÊNDICE C
Apresentamos o número de contêineres PI a serem reposicionados com base na suposição de que cada contêiner PI carrega 20,42 kg e pesa 4,5 kg, conforme descrito na Suposição 3 no texto principal.
Tabela C1: Desequilíbrios totais em toneladas entre regiões para cada um dos diferentes cenários (Situação atual, 1, 2, 3 e 4)
| Cenários de Compatibilidade | ||||||
|---|---|---|---|---|---|---|
| Regiões | Situação atual | 1 | 2 | 3 | 4 | |
| Norte–meio | 220.773,15 | – | 1.252.562,11 | 1.249.646,01 | 874.266,11 | |
| Norte–sul | 236.448,42 | 15.675,27 | 1.048.172,59 | 1.051.056,80 | 965.035,65 | |
| Meio–sul | 4.102.631,34 | 4.323.404,49 | 4.101.970,43 | 4.046.336,16 | 3.653.905,52 | |
Tabela C2: Número de PI-contêineres a serem reposicionados com base nos desequilíbrios apresentados na Tabela C1, assumindo que um PI-contêiner transporta 20,42 kg de carga
| Regiões | Cenários de Compatibilidade | ||||
|---|---|---|---|---|---|
| Como está | 1 | 2 | 3 | 4 | |
| Norte–meio | 10.811.613,5 | – | 61.339.966,2 | 61.197.160,3 | 42.814.207,4 |
| Norte–sul | 11.579.256,4 | 767.642,9 | 51.330.684,9 | 51.471.929,6 | 47.259.336,5 |
| Meio–sul | 200.912.406,5 | 211.724.020,0 | 200.880.040,8 | 198.155.541,7 | 178.937.586,6 |
Tabela C3: Peso total (em toneladas) de contêineres vazios a serem reposicionados dado o número de contêineres PI na Tabela C2 e assumindo que um contêiner PI pesa 4,5 kg
| Regiões | Cenários de Compatibilidade | ||||
|---|---|---|---|---|---|
| Condição Atual | 1 | 2 | 3 | 4 | |
| Norte–meio | 48.652,3 | – | 276.029,8 | 275.387,2 | 192.663,9 |
| Norte–sul | 52.106,7 | 3.454,4 | 230.988,1 | 231.623,7 | 212.667,0 |
| Meio–sul | 904.105,8 | 952.758,1 | 903.960,2 | 891.699,9 | 805.219,1 |
APÊNDICE D
Realizamos uma análise de sensibilidade para determinar se os padrões observados mudariam caso houvesse alterações na demanda. Os dados originais foram obtidos sob condições econômicas regulares. Assumimos que a demanda pode diminuir durante recessões econômicas. Assim, inicialmente consideramos o caso em que a demanda diminui em todas as regiões em certas proporções com base nos bens demandados nessas regiões. Em segundo lugar, assumindo que a demanda por itens alimentícios permanece a mesma mesmo durante uma recessão, consideramos reduções na demanda para todos os itens, exceto alimentos. Terceiro, consideramos o caso em que a demanda aumenta devido a um boom econômico. O aumento ou diminuição específica na demanda que consideramos é a seguinte:
• A demanda nos três hubs (sul, meio e norte) foi reduzida em 10%, 7,5% e 5%, respectivamente (considerando a sensibilidade geral do modelo).
• Não houve redução para os tipos de frete 2 e 10 (alimentos), redução de 10% em todos os outros tipos.
• A demanda nos três hubs (sul, centro e norte) aumentou em 10%, 7,5% e 5%, respectivamente (considerando a sensibilidade geral do modelo). Os resultados com demanda modificada mostram padrões muito semelhantes aos resultados com demanda original em todos os três casos, conforme mostrado nas Figuras D1–D3.



AUTORES
Henrik S. Sternberg (PhD, Chalmers University of Technology, Suécia) é Professor Assistente de Gestão da Cadeia de Suprimentos na Ivy College of Business, Iowa State University. Seus interesses de pesquisa são transparência na cadeia de suprimentos, política de transporte, eficiência logística, adoção de tecnologia e crowdsourcing em gestão de operações. A pesquisa do Dr. Sternberg é publicada, por exemplo, no Journal of Business Logistics, International Journal of Physical Distribution & Logistics Management, International Journal of Logistics Management e Transportation Journal.
Meltem Denizel (PhD, Warrington School of Business, University of Florida) é Professora Associada de Gestão da Cadeia de Suprimentos no Ivy College of Business, Iowa State University. Seus interesses de pesquisa são operações sustentáveis, eficiência da cadeia de suprimentos, modelagem matemática e dimensionamento de lotes de produção. A pesquisa da Dra. Denizel foi publicada, por exemplo, em Production and Operations Management, Operations Research, Decision Sciences, IIE Transactions, Transportation Journal e International Journal of Production Economics.
REFERÊNCIAS
ALICE2019. "Alliance for Logistics Innovation through Collaboration in Europe." ENIDE, accessed 25th of April. http://www.etp-logistics.eu/
Ambra, T., Caris, A., and Macharis, C. 2019. “Towards Freight Transport System Unification: Reviewing and Combining the Advancements in the Physical Internet and Synchromodal Transport Research.” International Journal of Production Research 57(6):1606–23.
Ambra, T., Caris, A., and Macharis, C. 2020. “Do You See What I See? A Simulation Analysis of Order Bundling within a Transparent User Network in Geographic Space.” Journal of Business Logistics Forthcoming 1–24. https://onlinelibrary. wiley.com/doi/10.1111/jbl.12237
Ballot, E., Bierlaire, M., Crainic, T.G., De Koster, R., Ellis, K.P., Fontane, F., Gendreault, M., Glardon, R., Gue, K.R., Hakimi, D., Heni, H., Labarthe, O., Lounes, M., Meller, R.D., Montreuil, B., Ogle, M., Smith, J., Shorabi, H., Th´emans, M., and Wieser, P. 2016. "The Physical Internet initiative." Mines ParisTech, accessed 2nd of January. http://www.physicalinte rnetinitiative.org/
Ballot, E., Gobet, O., and Montreuil, B. 2012. "Physical Internet Enabled Open Hub Network Design for Distributed Networked Operations." In Service Orientation in Holonic and Multi-Agent Manufacturing Control, edited by T. Borangiu, A. Thomas, and D. Trentesaux, 279–292. Warsaw, Poland: Springer.
Ballot, E., Montreuil, B., and Meller, R.D. 2014. The Physical Internet – The Network of Logistics Networks. Paris, France: La documentation Française. Ballot, E., Montreuil, B., and Thivierge, C. 2013. Functional Design of Physical Internet Facilities: A Road-Rail Hub. Montreal, Canada: CIRRELT.
Bartolacci, M.R., LeBlanc, L.J., Kayikci, Y., and Grossman, T.A. 2012. “Optimization Modeling for Logistics: Options and Implementations.” Journal of Business Logistics 33 (2):118–27.
Bergquist, M., Bernhardsson, V., and Rosklint, E. 2016. Representation of the Swedish Transport and Logistics System in Samgods v. 1.1. Linköping, Sweden: VTI.
Brax, S.A., Bask, A., Hsuan, J., and Voss, C.A. 2017. “Service Modularity and Architecture – An Overview and Research Agenda.” International Journal of Operations & Production Management 37(6):686–702.
Carbone, V., Rouquet, A., and Roussat, C. 2017. “The Rise of Crowd Logistics: A New Way to Co-Create Logistics Value.” Journal of Business Logistics 38(4):238–52.
Castillo, V.E., Bell, J.E., Rose, W.J., and Rodrigues, A.M. 2018. “Crowdsourcing Last Mile Delivery: Strategic Implications and Future Research Directions.” Journal of Business Logistics 39(1):7–25.
Chen, C., and Pan, S. 2015. "Using the Crowd of Taxis to Last Mile Delivery in E-commerce: A Methodological Research." SOHOMA’15, Cambridge, UK. CO3 Project. 2014. "CO3." NDL/HIDC, accessed October 11th. http://www.co3-project.eu/
Creemers, S., Woumans, G., Boute, R., and Beliën, J. 2017. “Tri-Vizor Uses an Efficient Algorithm to Identify Physical Internet—Logistics Service Modularity 159 Collaborative Shipping Opportunities.” Interfaces 47 (3):244–59.
de Blok, C., Meijboom, B., Luijkx, K., Schols, J., and Schroeder, R. 2014. “Interfaces in Service Modularity: A Typology Developed in Modular Health Care Provision.” Journal of Operations Management 32(4):175–89.
European Commission. 2016. Report from the Commission to the European Parliament and the Council. In COM (2016). Brussels, Belgium: European Commission.
Fazili, M., Venkatadri, U., Cyrus, P., and Tajbaksh, M. 2017. “Physical Internet, Conventional and Hybrid Logistic Systems: A Routing Optimisation-Based Comparison Using the Eastern Canada Road Network Case Study.” International Journal of Production Research 55(9):2703–30.
Hagebäck, C., and Segerstedt, A. 2004. “The Need for Co- Distribution in Rural Areas—A Study of Pajala in Sweden.” International Journal of Production Economics 89(2):153–63.
Hauder, V.A., Pitzer, E., and Affenzeller, M. 2018. “Optimization Approaches for the Physical Internet.” Lecture Notes in Computer Science 10697:236–45.
Hellström, D., and Nilsson, F. 2011. “Logistics-driven Packaging Innovation: A Case Study at IKEA.” International Journal of Retail and Distribution Management 39(9):638–57. Hesse, M., and Rodrigue, J.-P. 2004. “The Transport Geography of Logistics and Freight Distribution.” Journal of Transport Geography 12(3):171–84.
Hübner, A., and Ostermeier, M. 2019. “A Multi-Compartment Vehicle Routing Problem with Loading and Unloading Costs.” Transportation Science 53(1):282–300.
Jensen, A.F., Thorhauge, M., de Jong, G., Rich, J., Dekker, T., Johnson, D., Cabral, M.O., and Nielsen, O.A. 2019. “A Disaggregate Freight Transport Chain Choice Model for Europe.” Transportation Research Part E: Logistics and Transportation Review 121:43–62.
Jula, H., Chassiakos, A., and Ioannou, P. 2006. “Port Dynamic Empty Container Reuse.” Transportation Research Part E: Logistics and Transportation Review 42(1):43–60. Karlsson, R., and Bernhardsson, V. 2018. Calibration Report. Linköping, Sweden: VTI.
Kolar, P., Schramm, H.-J., and Prockl, G. 2018. “Intermodal Transport and Repositioning of Empty Containers in Central and Eastern Europe Hinterland.” Journal of Transport Geography 69:73–82.
Kuzmicz, K.A., and Pesch, E. 2019. “Approaches to Empty Container Repositioning Problems in the Context of Eurasian Intermodal Transportation.” Omega 85:194–213.
Landschutzer, C., Ehrentraut, F., and Jodin, D. 2015. “Containers for the Physical Internet: Requirements and Engineering Design Related to FMCG Logistics.” Logistics Research 8(8):1–22.
Landschützer, C., Jodin, D., and Ehrentraut, F. 2018. "Modular Boxes for the Physical Internet." Austria: Graz University of Technology, accessed October 14th. https://online.tugraz.a t/tug_online/voe_main2.getVollText?pDocumentNr= 901117&pCurrPk=81478
Ljungberg, A. 2013. “Impacts of Increased Rail Infrastructure Charges in Sweden.” Research in Transportation Economics 39(1):90–103.
Matusiewicz, M. 2020. “Logistics of the Future – Physical Internet and Its Practicality.” Transportation Journal 59 (2):200–14.
McKinnon, A.C., and Ge, Y. 2006. “The Potential for Reducing Empty Running by Trucks: A Retrospective Analysis.” International Journal of Physical Distribution & Logistics Management 36(5):391–410.
Meller, R.D., Montreuil, B., Thivierge, C., and Montreuil, Z. 2013. Functional Design of Physical Internet Facilities: A Road-Based Transit Center. Montreal, Canada: CIRRELT.
Mervis, J. 2014. “The information highway gets physical: The Physical Internet Would Move Goods the Way Its Namesake Moves Data.” Science 344(6188):1104–107.
MODULUSHCA 2016. Project Final Report: Modular Logistics Units in Shared Co-Modal Networks. Karlsruhe, Germany: PTV Group.
Mollenkopf, D., Closs, D., Twede, D., Lee, S., and Burgess, G. 2005. “Assessing the Viability of Reusable Packaging: A Relative Cost Approach.” Journal of Business Logistics 26 (1):169–97.
Montabon, F., Pagell, M., and Wu, Z. 2016. “Making Sustainability Sustainable.” Journal of Supply Chain Management 52(2):11–27.
Montreuil, B. 2011. “Toward a Physical Internet: Meeting the Global Logistics Sustainability Grand Challenge.” Logistics Research 3(2–3):71–87.
Montreuil, B., Ballot, E., and Tremblay, W. 2015. "Modular Design of Physical Internet Transport, Handling and Packaging Containers." Charlotte, NC: Progress in Material Handling Research.
Montreuil, B., Meller, R.D., Thivierge, C., and Montreuil, Z. 2013. Functional Design of Physical Internet Facilities: A Unimodal Road-based Crossdocking Hub. Montreal, Canada: CIRRELT.
Montreuil, B., Roug`es, J.-F., Cimon, Y., and Poulin, D. 2012. “The Physical Internet and Business Model Innovation.” Technology Innovation Management Review 2(6):32–37.
Pålsson, H., and Hellström, D. 2016. “Packaging Logistics in Supply Chain Practice – Current State, Trade-Offs and Improvement Potential.” International Journal of Logistics: Research and Applications 19(5):351–68.
Pålsson, H., and Sternberg, H. 2018. “High Capacity Vehicles and Modal Shift from Rail to Road: Combining Macro and Micro Analyses.” International Journal of Logistics: Research and Applications 21(2):115–32.
Pålsson, H., Winslott Hiselius, L., Wandel, S., Kahn, J., and Adell, E. 2017. “Longer and Heavier Road Freight Vehicles in Sweden – Effects on Tonne- and Vehicle-Kilometres, CO2 and Socio-Economics.” International Journal of Physical Distribution and Logistics Management 47(7):603–22.
Pan, S., Ballot, E., and Fontane, F. 2013. “The Reduction of Greenhouse Gas Emissions from Freight Transport by Pooling Supply Chains.” International Journal of Production Economics 143(1):86–94.
Pan, S., Ballot, E., Huang, G.Q., and Montreuil, B. 2017. “Physical Internet and Interconnected Logistics Services: Research and Applications.” International Journal of Production Research 55(9):2603–609.
160 H. S. Sternberg and M. Denizel Premkumar, G., Ramamurthy, K., and Crum, M. 1997. “Determinants of EDI Adoption in the Transport Industry.” European Journal of Information Systems 6(2):107–21.
Rai, H.B., Verlinde, S., Merckx, J., and Macharis, C. 2017. “Crowd Logistics: An Opportunity for More Sustainable Urban Freight Transport?” European Transport Research Review 9(3):39–52.
Rogers, D.S., Melamed, B., and Lembke, R.S. 2012. “Modeling and Analysis of Reverse Logistics.” Journal of Business Logistics 33(2):107–17.
Sallez, Y., Pan, S., Montreuil, B., Berger, T., and Ballot, E. 2016. “On the Activeness of Intelligent Physical Internet Containers.” Computers in Industry 81:96–104.
Salvador, F., Forza, C., and Rungtusanatham, M. 2002. “Modularity, Product Variety, Production Volume, and Component Sourcing: Theorizing beyond Generic Prescriptions.” Journal of Operations Management 20 (5):549–75.
Sandberg, K., Ado, A., Berntsson, S., Johansson, M., Melkersson, M., Petterson, H., Stelling, P., and Söderbaum, F. 2016. Godstransporter i Sverige – en nulägesanalys. edited by Brita Saxton. Stockholm, Sweden: Trafikanalys.
Sarraj, R., Ballot, E., Pan, S., Hakimi, D., and Montreuil, B. 2014a. “Interconnected Logistic Networks and Protocols: Simulation-based Efficiency Assessment.” International Journal of Production Research 52(11):3185–208.
Sarraj, R., Ballot, E., Pan, S., and Montreuil, B.. 2014b. “Analogies between Internet Network and Logistics Service Networks: Challenges Involved in the Interconnection.” Journal of Intelligent Manufacturing 25(6):1207–19.
Schilling, M.A. 2000. “Toward a General Modular Systems Theory and Its Application to Interfirm Product Modularity.” Academy of Management Review 25(2):312–34.
Shintani, K., Imai, A., Nishimura, E., and Papadimitriou, S. 2007. “The Container Shipping Network Design Problem with Empty Container Repositioning.” Transportation Research Part E: Logistics and Transportation Review 43 (1):39–59.
Simmer, L., Pfoser, S., Grabner, M., Schauer, O., and Putz, L.M. 2017. “From Horizontal Collaboration to the Physical Internet – A Case Study from Austria.” International Journal of Transport Development and Integration 1(2):129–36.
Song, D.-P. 2007. “Characterizing Optimal Empty Container Reposition Policy in Periodic-review Shuttle Service Systems.” Journal of the Operational Research Society 58 (1):122–33.
Stank, T.P., Pellathy, D.A., In, J., Mollenkopf, D.A., and Bell, J.E. 2017. “New Frontiers in Logistics Research: Theorizing at the Middle Range.” Journal of Business Logistics 38 (1):1–12.
Starr, M. 2010. “Modular Production – A 45-year-old Concept.” International Journal of Operations & Production Management 30(1):7–19.
Sternberg, H., and Norrman, A. 2017. “The Physical Internet – Review, Analysis and Future Research Agenda.” International Journal of Physical Distribution and Logistics Management 47(8):736–62.
Suzuki, Y., and Lu, S.-H. 2017. “Economies of Product Diversity in Collaborative Logistics.” Journal of Business Logistics 38(2):115–29.
Treiblmaier, H., Mirkovski, K., and Lowry, P.B. 2016. "Conceptualizing the Physical Internet: Literature Review, Implications and Directions for Future Research." 11th CSCMP Annual European Research Seminar, Vienna, Austria.
Treiblmaier, H, Mirkovski, K., Lowry, P.B., and Zacharia, Z.G. 2020. “The physical internet as a new supply chain paradigm: a systematic literature review and a comprehensive framework.” The International Journal of Logistics Management 31(2):239–87.
Tuunanen, T., Bask, A., and Merisalo-Rantanen, H. 2012. “Typology for Modular Service Design: Review of Literature.” International Journal of Service Science, Management, Engineering, and Technology 3(3):99–112.
Venkatesh, V., Morris, M.G., Davis, G.B., and Davis, F.D. 2003. “User Acceptance of Information Technology: Toward a Unified View.” MIS Quarterly 27(3):425–78.
Vierth, I., Mellin, A., Hyl´en, B., Karlsson, J., Karlsson, R., and Johansson, M. 2012. Kartläggning av godstransporterna i Sverige. In VTI Rapport. Linköping, Sweden: VTI.
Voss, C.A., Perks, H., Sousa, R., Witell, L., and Wünderlich, N.V. 2016. “Reflections on Context in Service Research.” Journal of Service Management 27(1):30–36.
Wall, J. 2013. Missing Link 2013. Gothenburg, Sweden: Ramböll.
Waller, M.A., and Fawcett, S.E. 2012. “Mathematical Modeling in Logistics: In for a Penny, in for a Pound.” Journal of Business Logistics 33(2):78–79.
Yang, Y., Pan, S., and Ballot, E. 2017. “Mitigating Supply Chain Disruption through Interconnected Logistics Services in the Physical Internet.” International Journal of Production Research 55(14):3970–83.
Yun, W.Y., Lee, Y.M., and Choi, Y.S. 2001. “Optimal Inventory Control of Empty Containers in Inland Transportation System.” International Journal of Production Economics 133 (1):451–57.


















