Hacia el Internet Físico: modularidad de los servicios logísticos e implicaciones de diseño
INTRODUCCIÓN
Los desafíos económicos, sociales y, quizás lo más importante, ambientales de las cadenas de suministro actuales exigen nuevos enfoques para la gestión de la cadena de suministro (Montabon et al. 2016). El éxito de proyectos de colaboración horizontal como CO3 (Proyecto CO3 2014) y proyectos de colaboración liderados por la industria (Creemers et al. 2017) ha inspirado el desarrollo del Internet Físico (PI o π; Montreuil 2011; Mervis 2014). El PI es un concepto innovador que utiliza el Internet Digital como metáfora para recursos compartidos como el transporte y el almacenamiento, con la carga encapsulada en contenedores PI (Landschutzer et al. 2015; MODULUSHCA 2016) y transportada a través de un protocolo estándar (Montreuil et al. 2012; Ballot et al. 2014). En comparación con el sistema logístico convencional, el PI representa un sistema radicalmente diferente (Ballot et al. 2014; Ambra et al. 2020) que obligará a los actores privados y públicos a replantear sus estrategias de cadena de suministro.
Grandes responsables políticos como la Comisión Europea han adoptado el PI como la visión objetivo para la logística europea en 2050; a nivel mundial, importantes actores de la industria, asociaciones y autoridades se están uniendo a la iniciativa estratégica ALICE[1] en un esfuerzo por difundir el Internet Físico (Pan et al. 2017; ALICE 2019; Ambra et al. 2019). Varios estudios han descrito mejoras potenciales enormes tanto a través del concepto PI como del área adyacente de compartir transporte y almacenamiento (Pan et al. 2013; Creemers et al. 2017). Ballot et al. (2012) reportaron una reducción del 20% en el consumo de combustible; Sarraj et al. (2014a) señalaron una posible reducción del 60% de CO2; y Yang et al. (2017) mostraron que el costo logístico podría, en algunos casos, reducirse hasta en un 73%. Debido a que el Internet Físico promete mejorar la sostenibilidad económica, ambiental y social, y atraer una inversión pública y privada significativa, su adopción y efectos anticipados son altamente relevantes para profesionales, responsables políticos y académicos por igual (Sternberg y Norrman 2017; ALICE 2019).
La automatización terminal (es decir, la carga y descarga automatizadas) permite un nuevo paradigma en el diseño de la red de la cadena de suministro, ya que los profesionales de la cadena de suministro hoy en día intentan evitar los riesgos y desperdicios asociados con la carga y descarga (Hübner y Ostermeier 2019). Hoy en día, la falta de embalajes estandarizados, como los contenedores PI, es una barrera para la automatización terminal, obstaculizando las posibles ganancias de eficiencia (Mervis 2014; Montreuil et al. 2015).
Según Montreuil et al. (2015), “El Internet Físico trata estrictamente con bienes encapsulados en contenedores modulares estándar π que deben ser el equivalente material a los paquetes de datos [del Internet Digital]” (p.2). Los contenedores PI estarán disponibles en muchas variaciones y tamaños y acomodarán prácticamente todo tipo de productos (Montreuil et al. 2013) y unidades de carga. La capacidad de una cadena de suministro para reposicionar eficientemente o realizar cargas de retorno de embalajes retornables como un contenedor PI depende en gran medida de las características del embalaje retornable. El embalaje con características específicas que lo hagan incompatible con la carga de otros tipos de bienes causará un aumento en viajes en vacío (McKinnon y Ge 2006). Dado que los contenedores PI tienen diferentes tamaños y no están centralmente enrutados, Sternberg y Norrman (2017) enfatizan la importancia estratégica de analizar el efecto de múltiples contenedores PI en los balances de carga, porque reposicionar embalajes retornables o cualquier tipo de contenedor es crucial para estimar con precisión las ganancias de eficiencia (Mollenkopf et al. 2005; Kolar et al. 2018; Kuzmicz y Pesch 2019).
A pesar del potencial y la investigación significativa sobre el PI (Ballot et al. 2016), Treiblmaier et al. (2016) señalan que la investigación sobre el Internet Físico generalmente no ha incorporado teoría y que la base teórica está “altamente subdesarrollada” (p. 15). Hasta donde sabemos, los protocolos detallados, paquetes (contenedores PI) e interfaces definidos en los planos del PI (cf., Meller et al. 2013; Ballot et al. 2014) lo convierten en la modularización de servicios más extensamente especificada (Starr 2010) conocida en el campo de la gestión de la cadena de suministro.
El propósito de este artículo fue analizar los contenedores PI desde una perspectiva logística estratégica (Bartolacci et al. 2012). Nos basamos en la teoría de la modularidad de servicios para enmarcar antecedentes a los futuros efectos del Internet Físico, respondiendo a varias solicitudes de investigación sobre el Internet Físico (Treiblmaier et al., 2020; Pan et al. 2017; Sternberg y Norrman 2017; Ambra et al. 2019).
Dado que el objetivo del Internet Físico es afrontar el gran desafío de sostenibilidad de la logística (Montreuil 2011), el efecto del reposicionamiento de contenedores PI determina los beneficios futuros, un factor crucial que determina la intención de adoptar estratégicamente nuevas innovaciones (Premkumar et al. 1997; Venkatesh et al. 2003). Por lo tanto, como punto de partida para investigar los efectos de las características de los contenedores PI, planteamos la siguiente pregunta de investigación: ¿Cuáles son las implicaciones de la modularidad del servicio del Internet Físico en los flujos de contenedores PI? En otras palabras, ¿cómo afecta el nivel de modularidad del servicio (o la compatibilidad del contenedor PI en el transporte regional) a los flujos de contenedores PI y, más específicamente, al reposicionamiento de los contenedores PI? Contribuimos a las discusiones en curso con ideas tanto para los responsables de políticas como para los investigadores de la cadena de suministro en las áreas de estrategia del Internet Físico y teoría contextualizada de rango medio (Stank et al. 2017) de la modularización del servicio logístico (Voss et al. 2016). Además, ampliamos la literatura tradicional sobre el reposicionamiento de contenedores marítimos elaborando sobre las especificidades de los contenedores PI. Debido a que el Internet Físico aún no existe, esta investigación es conceptual; sin embargo, usamos datos empíricos en un modelo de programación lineal para analizar los efectos esperados, un enfoque metodológico comúnmente utilizado para el reposicionamiento de contenedores marítimos (Shintani et al. 2007; Kuzmicz y Pesch 2019). Se utiliza la teoría de Sistemas Modulares Generales de Schilling (2000) para enmarcar los resultados.
El enfoque de este artículo es la modularidad y la logística de embalaje (entrada en el sistema modular) en el transporte intrarregional de carga general, es decir, transporte de terminal a terminal. Por lo tanto, los problemas de primer y último tramo quedan fuera del alcance de este artículo. Como se discutirá, examinamos los efectos logísticos estratégicos en un sistema híbrido (Fazili et al. 2017), centrado en el nivel estratégico de la demanda, el suministro y el transporte. Dado que solo aproximadamente el 1 % de la carga general en Suecia se transporta por ferrocarril (Sandberg et al. 2016), nuestro análisis se centra en el transporte por carretera de carga general. Nuestros resultados destacan la importancia de mantener la modularidad del servicio en el sistema de transporte, mostrando que la carga conjunta del Internet Físico representa una mejora en la eficiencia que compensa el material adicional de embalaje que se debe transportar. Sin embargo, nuestros resultados también subrayan que si la modularidad del servicio se reduce debido a la falta de compatibilidad en el embalaje del transporte, las ganancias de eficiencia no se materializan. Esto es de gran importancia para la futura estrategia de la gestión de la cadena de suministro y la formulación de políticas, ya que enfatiza las condiciones en las que el Internet Físico es parte de la solución al gran desafío.
LITERATURA RELACIONADA
Esta sección describe algunos de los conceptos relacionados con PI: logística de embalajes y tasas de llenado, los componentes del PI y la modelización del reposicionamiento de contenedores marítimos. Para una discusión más amplia o general del concepto, véase el libro de Ballot et al. (2014) sobre PI o la reciente revisión bibliográfica de Treiblmaier et al. (2020).
Logística de embalajes y tasas de llenado
El embalaje generalmente se refiere a diferentes niveles de embalaje en el sistema logístico. El embalaje primario está más cercano al producto y suele ser el embalaje para el consumidor o para la venta. El embalaje secundario contiene un cierto número de embalajes primarios, a menudo denominado embalaje comercial. El embalaje terciario contiene varios embalajes secundarios, y a menudo se refiere como embalaje de transporte, como el euro pallet. La logística de embalajes se centra en las sinergias logradas mediante la integración de los sistemas de embalaje y la logística (Pålsson y Hellström 2016).
Los flujos de transporte equilibrados son una de las claves para altas tasas de llenado y un transporte de carga sostenible, sin embargo, los desequilibrios de carga caracterizan la logística en la mayoría de las partes del mundo (Hesse y Rodrigue 2004). Los flujos desequilibrados y la circulación en vacío son aún más comunes en ciertas partes del proceso de distribución, como la logística de la primera y última milla. En distancias más largas, equilibrar los flujos se vuelve más importante. Por ejemplo, en Escandinavia, los flujos hacia el norte y hacia el sur en Noruega, Suecia y Finlandia difieren en gran medida tanto en términos de volumen como de tipos de bienes transportados (Vierth et al. 2012; Wall 2013). Por lo tanto, poder transportar diferentes tipos de bienes según la dirección de los flujos interregionales es crucial. McKinnon y Ge (2006) analizaron el potencial de cargas de retorno en el Reino Unido y encontraron que la incompatibilidad de vehículos y productos (es decir, el embalaje) fue uno de los factores principales detrás de la circulación en vacío.
Componentes del internet físico
Según investigadores como Ambra et al. (2019) y Matusiewicz (2020), el Internet Físico, la visión para la logística para 2050, contiene una hoja de ruta detallada del desarrollo del concepto y hitos significativos a través de ALICE (2019). En esta sección, elaboramos sobre la infraestructura PI y los contenedores PI.
Infraestructura PI
Ambra et al. (2019) describen la mecánica del Internet Físico de la siguiente manera: “El PI está inspirado en la metáfora del Internet Digital que utiliza conmutación de paquetes; el mensaje se divide en diferentes piezas (paquetes) que viajan por internet a través de varias rutas y luego se reúnen en el lado del receptor. Los paquetes son dirigidos a través de una red interconectada de nodos/hubs (PI-hubs) dependiendo de la capacidad de la red. Este enfoque de desmantelamiento está siendo adaptado por el PI donde los bienes físicos o, en términos más generales, los objetos físicos pueden ser dirigidos a través de diferentes enlaces desde sus orígenes hasta los destinos en contenedores estandarizados usando procedimientos de manipulación estandarizados” (p. 1607).
Varios artículos sobre PI han tratado los protocolos (Montreuil et al. 2012; Sarraj et al. 2014a) y el enrutamiento (Ballot et al. 2012; Sarraj et al. 2014b). Como todos los hubs serán interoperables, una ventaja distintiva del Internet Físico sería que virtualmente todos los carriles podrían ser transitados por camiones llenos, una gran razón para las mejoras del concepto previamente descritas en relación con los sistemas convencionales. Los PI-hubs están diseñados para manejar de manera automática la entrada y salida de los contenedores PI (ver Figura 1; Ballot et al. 2013).
Debido a su anticipada manipulación rápida y autónoma, las ventanas de tiempo pierden su importancia relativa (cf. cómo el Internet Digital envía paquetes de datos) porque las restricciones en el transporte terminal a terminal solo se convierten en una preocupación importante cuando los bienes van de un terminal a un consignatario.
Contenedores PI (PI-containers)
El sistema de contenedores PI es una parte integral del Internet Físico (Montreuil 2011; Ballot et al. 2014). Todos los bienes se envasan en contenedores PI, que son apilables y pueden ser manejados en PI-hubs automatizados (Montreuil et al. 2013). Sallez et al. (2016) describen las tres categorías principales de contenedores PI. Los contenedores de embalaje, los más cercanos al producto, son el embalaje primario. Los contenedores de manipulación contienen un producto individual, un grupo de productos o varios contenedores de embalaje (embalaje secundario). Finalmente, los contenedores de transporte contienen los contenedores de manipulación para su transporte (embalaje terciario). Se asume que los contenedores PI reemplazarán a los pallets sobre los cuales se puede cargar diferentes tipos de carga. Las muñecas rusas se utilizan frecuentemente para ilustrar el anidamiento de los contenedores PI (Montreuil 2011).
El artículo de Landschutzer et al. (2015) y el informe final del proyecto MODULUSHCA de la Comisión Europea (2016) describen dos casos de contenedores PI: el contenedor de manejo denominado m-box (ver Figura 2) y el contenedor de transporte referido como contenedor PI de carga unitaria. Los m-boxes se cargan dentro del contenedor PI de carga unitaria, y estos contenedores se cargan en un remolque EU (Landschutzer et al. 2015). El m-box del proyecto MODULUSHCA se ajusta a los remolques estándar europeos (estándar europeo máximo de longitud 16,5 m, peso máximo (camión + remolque) 40 toneladas). Sin embargo, si se usan con TEUs, el uso de las cajas generaría mucho espacio vacío (debido a la incompatibilidad inherente de los pallets EU y los TEUs), un problema que aún no se ha resuelto.


Aunque los m-boxes actualmente no son plegables, se espera que la función de plegado esté disponible en la próxima generación (MODULUSHCA 2016). Los contenedores PI plegables son compatibles, ya que los contenedores PI plegados pueden reposicionarse con cualquier categoría de mercancías.
La literatura sugiere dimensiones adicionales posibles para los contenedores PI, que se asumen apilables, lo que permite altas tasas de llenado en los contenedores PI de carga unitaria. Sarraj et al. (2014a) proponen un conjunto de contenedores PI modulares con diferentes tamaños (2.4 m*2.4 m* [1.2, 2.4, 3.6, 4.8, 6, 12] m). Esta modularidad se basa en el contenedor “ancho pallet” (PW), que es una unidad de transporte intermodal usada en Europa. Según Sarraj et al. (2014a), estos tamaños representan tamaños potenciales. Usando estos tamaños, ellos proporcionan una formulación del problema Bin Packing (BPP) para empacar los contenedores PI por modos de transporte (por ejemplo, camiones) (Sarraj et al. 2014a).
Para estudiar problemas de interrupciones en los PI-hubs, Yang et al. (2017) utilizaron los mismos tamaños de contenedores PI y protocolos de embalaje de contenedores PI (especificando cómo asignar la carga al contenedor PI de mejor ajuste). Hauder et al. (2018) también sugieren usar el problema BPP para asignar contenedores PI a los PI-movedores (modos de transporte).
Reposicionamiento de contenedores
Se esperan desequilibrios de flujo entre diferentes regiones en la red y la necesidad resultante de equilibrar los flujos de contenedores PI, como en cualquier sistema. En el PI, se espera que los contenedores sean comúnmente utilizados por todas las compañías navieras. Por lo tanto, el reposicionamiento de contenedores PI es en teoría más fácil, aunque necesario debido a tipos de carga incompatibles y desequilibrios comerciales entre las áreas geográficas donde se encuentran los hubs PI. Un estudio reciente de Kolar et al. (2018), basado en un estudio de caso en el país sin salida al mar República Checa, sugiere que en la práctica, el reposicionamiento de contenedores vacíos se percibe más como un problema de desequilibrio comercial global que como un problema de asignación integrada de recursos o equipos y enrutamiento de vehículos. Debido a esta percepción, los transportistas oceánicos se enfocan principalmente en soluciones a nivel global más que regional. En la literatura, diferentes aspectos del problema de reposicionamiento de contenedores vacíos han sido abordados utilizando modelado matemático y programación lineal o estocástica (por ejemplo Yun et al. 2001; Jula et al. 2006; Song 2007). Kuzmicz y Pesch (2019) ofrecen una revisión detallada de los enfoques de optimización para el problema en términos de reposicionamiento de contenedores TEU y FEU.
La programación lineal, que es uno de los enfoques comúnmente utilizados (Kuzmicz y Pesch 2019), asume demandas deterministas y provee soluciones de costo mínimo para reposicionamiento bajo diferentes políticas de reutilización de contenedores. En el contexto del PI, el reposicionamiento de contenedores vacíos también puede presentar un problema en términos de los contenedores PI. Aunque se asume que los contenedores PI vienen en diferentes tamaños, los tipos de carga incompatibles y los desequilibrios comerciales aún pueden hacer necesaria la reposición de contenedores PI vacíos. Considerando la compatibilidad de los contenedores PI en su capacidad para contener (o ser transportados junto con) diferentes tipos de carga, estudiamos cuánto reposicionamiento de contenedores PI vacíos se requeriría bajo diferentes escenarios de compatibilidad. Como se articula en Rogers et al. (2012), la programación lineal es adecuada para el análisis de escenarios mediante el cambio de los parámetros de interés.
MARCO TEÓRICO: MODULARIDAD EN LOS SERVICIOS LOGÍSTICOS
La modularidad se considera una forma de aumentar la común denominación entre diferentes versiones o variantes de un producto dentro de un sistema o familia de productos, es decir, permitir que el mismo(os) componente(s) se utilice(n) en varias variantes de producto (Schilling 2000; Salvador et al. 2002). Un sistema puede definirse no solo a nivel de industria u organización, sino también a nivel de producto (bien o servicio) para ser proporcionado al cliente (Schilling 2000). Tuunanen et al. (2012) definen un módulo de servicio como “un sistema de componentes que ofrece una funcionalidad bien definida a través de una interfaz descrita con precisión y con el cual un servicio modular se compone, adapta, personaliza y customiza” (p.102).
Las interfaces son los mecanismos que integran los subsistemas en un todo. En este sentido, las interfaces aseguran un acoplamiento débil, lo cual permite que los subsistemas funcionen independientemente y posibilita la sustitución de subsistemas según sea necesario para modificar el propio sistema. Salvador et al. (2002) explican: “Como tal, una motivación subyacente en la corriente de investigación de gestión de operaciones ha sido entender los beneficios de la común denominación de componentes en el desempeño operativo, así como los diversos factores que podrían afectar estos beneficios” (p. 551).
Schilling (2000) ha esbozado un modelo para describir los factores que impulsan la integración (disminución de la modularidad) y la desagregación (aumento de la modularidad): “En su nivel más abstracto, se refiere simplemente al grado en que los componentes de un sistema pueden separarse (separabilidad) y recombinarse” (p. 315). El marco de modularidad de Schilling contiene los siguientes componentes:
- Heterogeneidad de los insumos se refiere a la facilidad o dificultad del sistema para modularizarse. Los insumos en un sistema de servicios incluyen tanto las opciones tecnológicas disponibles para lograr funciones particulares como los recursos y capacidades de las empresas involucradas en la producción del servicio. Por ejemplo, las características del aceite a granel caliente y del pescado congelado son muy diferentes. Estos insumos heterogéneos requieren equipos de transporte especializados (cisterna de alimentos y remolque congelador, respectivamente), lo que los hace difíciles de modularizar. Sin embargo, en el escenario del aceite a granel caliente y el pescado congelado, si un sistema modular fuera capaz de manejar estos insumos heterogéneos en el mismo sistema, dicho sistema podría materializar ganancias significativas en la eficiencia del transporte.
- Heterogeneidad de las demandas se refiere al nivel de diferencias entre las demandas de los clientes. Cuanto más similares sean las demandas de los clientes, más se inclinará el sistema a aumentar la modularización.
- La especificidad sinérgica del sistema crea presión en contra de que el sistema migre hacia la modularidad. Los insumos heterogéneos en combinación con demandas heterogéneas reforzarán el efecto mutuo, creando una especificidad sinérgica hacia menor modularidad.
- Urgencia se refiere al cambio tecnológico (o la velocidad del mismo) y a la intensidad competitiva. Los fabricantes con ventas lucrativas en el mercado posventa tratarán de mantener el statu quo y trabajarán en contra de la modularización. Por otro lado, autoridades como la Comisión Europea intentarán imponer la modularidad mediante interfaces abiertas y estándares (por ejemplo, Comisión Europea 2016).
Schilling (2000) también argumenta que los sistemas en general se caracterizan por la inercia y que no responden de forma inmediata y vigorosa. Revisando más de 45 años de modularidad en el campo de la gestión de operaciones, Starr (2010) explica que la modularización en la industria manufacturera no había alcanzado la adopción anticipada porque la fabricación de bajo costo en el extranjero representaba un ahorro relativamente mayor para la industria. Sin embargo, la modularización en el contexto de los servicios de transporte generalmente no requiere cambios de ingeniería en los productos, aunque existen excepciones que pueden ser altamente beneficiosas (Hellström y Nilsson 2011). Aunque estos cambios pueden volverse muy costosos, alteran la manera en que los productos son manejados y transportados. Los contenedores PI y los hubs PI del Internet Físico pueden proporcionar estos medios.
Schilling (2000) define la acción principal para aumentar la modularidad como la capacidad de combinar y recombinar insumos heterogéneos en una variedad de configuraciones heterogéneas y sugiere que “⋯, la heterogeneidad en la variedad de insumos, combinada con la heterogeneidad en los clientes, crea incentivos poderosos para adoptar un sistema modular” (p. 317). En el contexto de un sistema logístico, debido a la heterogeneidad de los insumos (bienes), se utilizan diferentes paquetes o contenedores. Estos paquetes específicos para los bienes pueden considerarse componentes de un sistema modular que pueden separarse y recombinarse. Por ejemplo, el contenido de un contenedor (paquetes o contenedores PI) entregados a un hub puede separarse y enviarse fuera del hub hacia otro hub o hacia sus destinos finales. En contraste con la modularidad del producto, la modularidad del servicio generalmente no corre el riesgo de perder ninguna funcionalidad de transporte porque está commoditizada y porque la mayoría de los receptores de bienes tienen demandas homogéneas.
Por otra parte, la especificidad sinérgica, como un factor esperado para disminuir la modularidad, puede ser un obstáculo cuando los paquetes con la misma etiqueta de origen y destino no pueden combinarse de manera efectiva en la misma unidad de carga. Por ejemplo, supongamos que se crea un contenedor PI, como un tambor de petróleo, para encapsular un tipo de bien.
Estos contenedores PI para tambores deben ser devueltos a un sitio de producción después de que el aceite haya sido consumido en la ubicación de la demanda. Si la ubicación produce bienes envasados en contenedores PI (como m-boxes) que no pueden plegarse, la cadena de suministro enfrenta un doble flujo de mercancías porque el respectivo reposicionamiento de cada tipo de contenedor PI sería incompatible con el flujo regular, es decir, generando un desequilibrio de flete porque el reposicionamiento de los contenedores PI no es separable. Por lo tanto, si los flujos de contenedores PI tienen un bajo nivel de compatibilidad, es poco probable que el Internet Físico sea la estrategia elegida por los transportistas, quienes no querrían pagar un cargo adicional por el reposicionamiento de los contenedores PI vacíos (es decir, el bajo nivel de compatibilidad representa especificidad sinérgica).
Según el marco de Schilling (2000), la urgencia es el último factor que afecta la adopción de la modularidad. En logística, la urgencia proviene de las demandas de sostenibilidad ambiental y social que presionan a los transportistas a cambiar sus métodos. La urgencia también es posibilitada y motivada por cambios tecnológicos como la computación en la nube y el Internet de las cosas. Es importante destacar que la modularidad en el Internet Físico es paradójica porque los contenedores PI, aunque ejemplifican claramente la modularización, también corren el riesgo de amplificar la heterogeneidad de los insumos. Con el aumento de la heterogeneidad de los insumos (que causa flujos incompatibles de contenedores PI), la modularidad del servicio puede verse afectada negativamente. En este manuscrito, investigamos el efecto de estos factores en los flujos de contenedores PI del Internet Físico. Asumimos que la heterogeneidad tanto en términos de insumos como de productos finales (demanda del cliente) permanece constante en la industria logística. Por lo tanto, nos centramos en la especificidad sinérgica en términos de compatibilidad de los contenedores PI y en la urgencia en términos de uso de tecnología y sostenibilidad ambiental.
DISEÑO DE INVESTIGACIÓN
En el contexto de la modularización de servicios y la logística de empaques, nuestro estudio utiliza modelado matemático para abordar los efectos estratégicos logísticos de los flujos de contenedores PI del Internet Físico. Con un trabajo extenso realizado en algunos aspectos del concepto pero muy poco sobre contenedores PI (Treiblmaier et al., 2020; Sternberg y Norrman 2017) y una investigación previa sobre el reposicionamiento de contenedores marítimos, el estado actual del PI sugiere que es apropiado elaborar sobre los efectos del reposicionamiento del sistema de contenedores PI utilizando modelado matemático (Shintani et al. 2007; Rogers et al. 2012; Kuzmicz y Pesch, 2019).
Este artículo ofrece un análisis estratégico de los volúmenes totales y balances de flete y contenedores PI en una red terminal a terminal. Los resultados están destinados a ofrecer implicaciones estratégicas sobre los efectos de la adopción del PI para los gestores de la cadena de suministro y responsables políticos. Por lo tanto, nuestro modelo determinista no examina operaciones, estacionalidad u otros factores temporales, sino que se centra en la cuestión más importante (desde la perspectiva de la adopción) del efecto general de las características del contenedor PI. Como señalaron Waller y Fawcett (2012), un desafío en la aplicación de modelado matemático para generar teoría en la cadena de suministro y logística ha sido a menudo que las implicaciones y supuestos han vuelto los modelos menos útiles o poco prácticos. Para superar este desafío, hemos consultado diversos expertos y profesionales de la industria logística y hemos observado cuidadosamente los flujos del estudio que están siendo modelados. Los resultados de nuestras consultas forman los supuestos de esta investigación. Sin embargo, antes de describir el modelo y los supuestos, discutiremos el conjunto de datos, SAMGODS.
Datos y justificación - SAMGODS
Para analizar los posibles efectos del PI a través de la demanda derivada para la distribución, utilizamos Suecia como un caso cuantitativo. Debido a que los países vecinos tienen flujos de carga similares y respectivas diferencias en el transporte de norte a sur, incluir datos de esos países no produciría resultados diferentes en términos de los efectos relativos del nivel de compatibilidad de los contenedores PI. Todos los volúmenes nacionales cargados y descargados en Suecia se obtuvieron utilizando los datos SAMGODS (Vierth et al. 2012; Bergquist et al. 2016; Karlsson y Bernhardsson 2018), cortesía de la Administración de Tráfico Sueca. Es una matriz origen-destino de todos los flujos de carga nacionales en Suecia, con un municipio como origen y destino. Los datos del SAMGODS se han utilizado en numerosos estudios en la última década (por ejemplo, Ljungberg 2013; Pålsson et al. 2017; Pålsson y Sternberg 2018; Jensen et al. 2019), y Karlsson y Bernhardsson (2018) han explicado su calibración. Ubicada en la esquina de Europa, Suecia ofrece acceso a datos de carga de alta calidad, tiene largas distancias de carga y ha recibido mucha atención en la investigación; por lo tanto, Suecia es adecuada para el análisis del PI.
Los datos SAMGODS dividen la carga en 35 categorías, basándose en sus características (por ejemplo, paletizado, tanque, granel seco) y el tipo de vehículo requerido (por ejemplo, remolque frigorífico, vehículo para madera). Para calcular los efectos del Internet Físico en los balances de carga en Suecia, nos centramos en las 12 categorías de carga en los datos SAMGODS que se transportan en las mismas combinaciones de vehículos que la carga general.
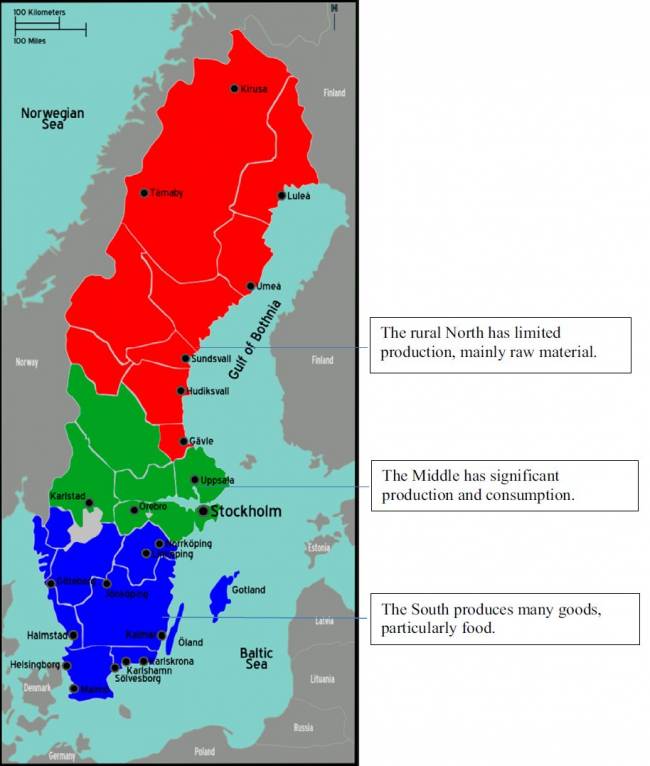
Las 12 categorías se seleccionaron en colaboración con expertos de la industria y tras inspecciones visuales de los flujos de norte a sur y de sur a norte. Usamos las tres regiones geográficas de Suecia como representación de los flujos de carga intra-regionales (ver Figura 3). Estas regiones representan una diversidad significativa en términos de oferta y demanda de bienes. La Figura 3 ofrece una visión simplificada de la oferta y demanda regional de bienes en Suecia.
En términos de modularidad, la compatibilidad entre diferentes transportes de contenedores PI determina si el Internet Físico disminuirá la modularidad (como se describió en la sección anterior). Las futuras implementaciones del Internet Físico podrían incluir contenedores PI adoptados para bienes a granel, lo que significaría que PI posiblemente aumentaría la modularidad. Sin embargo, tales implementaciones son más probables que aparezcan después de que se haya alcanzado una masa crítica de centros PI y operadores participantes.
Contribuciones de expertos a las suposiciones
La calidad de cualquier modelo depende de las suposiciones subyacentes (Waller y Fawcett 2012); por lo tanto, consultamos con seis expertos en distribución física entre 2012 y 2018 (Tabla 1). Estos expertos fueron seleccionados en base a su competencia y experiencia en logística del mundo real, con un enfoque específico en operaciones terminal a terminal en operaciones nacionales suecas.
Tradicionalmente, los modelos matemáticos se validan con datos del mundo real. Debido a que no existe un Internet Físico real, no hay datos reales para validar el modelo, lo que aumenta la importancia de utilizar datos de entrada confiables y supuestos apropiados al analizar el Internet Físico.
EL MODELO
Basándonos en nuestra pregunta de investigación y en los datos SAMGODS, formulamos un modelo matemático que imita el Internet Físico. El modelo tiene como objetivo minimizar los desequilibrios en los flujos de contenedores PI entre los hubs PI. Como se discutió anteriormente, los desequilibrios en los flujos pueden deberse a desequilibrios comerciales entre las regiones o a diferentes tipos de carga que necesitan diferentes tipos de contenedores PI. Suponemos que la cantidad (en toneladas) y los tipos de carga que un hub debe suministrar a otros hubs indican su demanda de la cantidad (en toneladas) y los tipos de contenedores PI. De manera similar, la cantidad (en toneladas) y los tipos de carga que un hub debe recibir de otros hubs indican su oferta de la cantidad (en toneladas) y los tipos de contenedores PI.
Una vez que se conocen las características (tamaño y peso) del contenedor PI utilizado para una categoría específica de carga, se puede calcular el número de contenedores PI de ese tipo (basado en el tamaño) para la cantidad que se va a transportar en ese tipo/tamaño de contenedor PI. Basándonos en los supuestos del PI, asumimos que los contenedores PI se enrutan automáticamente a través de diferentes rutas desde sus orígenes hasta los destinos (nuestro enfoque es el transporte de terminal a terminal). El objetivo es mover los contenedores PI entre terminales mientras se minimizan los flujos inversos, es decir, el reposicionamiento de contenedores PI vacíos. Nuestro modelo es aplicable al transporte interregional en un Internet Físico y no depende de si la primera y última milla al respectivo hub regional PI se realiza en el PI o mediante transporte convencional (Fazili et al. 2017).
| Experto # | Datos | Conclusiones y notas especiales | Contribución a las suposiciones |
|---|---|---|---|
| 1. Consultor macro senior de transporte | Dos entrevistas y varios correos electrónicos 2016–2017 | El consultor macro senior ayudó a los investigadores a proponer tipos de carga compatibles y a realizar agregaciones correctas de los datos SAMGODS. El consultor revisó una versión anterior de este artículo. | #3 & 6 |
| 2. Gerente de distrito (proveedor internacional de servicios logísticos) | Entrevista telefónica 2012 | El gerente de distrito explicó la colaboración horizontal y vertical entre los proveedores de servicios logísticos y los clientes en el norte rural de Suecia. | #2 |
| 3. CEO y 4. Jefe de Relaciones con Miembros (Asociación de Transportistas) |
Varias reuniones presenciales y telefónicas 2016–2018 | La asociación de transportistas representa a más de 100 empresas de transporte por carretera que operan servicios de línea y distribución para un proveedor logístico importante. El CEO y el jefe de Relaciones con Miembros proporcionaron información valiosa sobre cómo sus empresas asociadas operan sus líneas en el sistema hub-and-spoke del proveedor logístico. | #2, 3, & 7 |
| 5. Gerente de operaciones de transportista por carretera operando una terminal | Dos entrevistas telefónicas y varios correos electrónicos 2017 | El gerente de operaciones de este transportista por carretera en el norte de Suecia administra un hub y supervisa la carga de mercancías con dirección sur y la descarga de mercancías con dirección norte. Durante más de dos semanas, el gerente de operaciones tomó fotografías sistemáticas de la carga de todos los camiones entrantes y salientes. | #2, 3, & 6 |
| 6. Conductor (proveedor nacional logístico importante) | Varias discusiones informales 2017 | Un conductor empleado por un proveedor logístico nacional importante tomó, con permiso, fotografías de todos los camiones salientes de la terminal de Gotemburgo. Este conductor tiene más de 20 años de experiencia con todo tipo de vehículos y ha participado en numerosos proyectos de investigación y desarrollo sobre la eficiencia de los conductores. Fue informado sobre el Internet Físico; ayudó como interlocutor de discusión; y proporcionó información sobre tasas de llenado, embalajes y suposiciones de peso. | #3 |
El modelo es lo suficientemente general para manejar cualquier número de nodos en la red interconectada de PI-hubs y cualquier número de tipos de carga. Un aspecto importante que queremos analizar es la compatibilidad del flujo de PI-containers con la carga real. Para este propósito, nuestro modelo maneja cuatro escenarios de compatibilidad como se detalla a continuación, donde K indica el número de tipos de carga, y C indica el número de grupos compatibles de PI-containers.
• Con compatibilidad total, que es el mejor caso, todos los tipos de carga pueden combinarse de modo que solo haya un (C = 1) tipo de PI-container que debe ser considerado.
• Sin compatibilidad, que es el peor caso, cada tipo de carga debe transportarse por separado en C = K diferentes tipos de PI-containers.
• Con compatibilidad limitada, que está más cerca del caso sin compatibilidad, la carga debe transportarse en C = 2K/3 diferentes tipos de PI-containers.
• Con algo de compatibilidad, más cerca del caso de compatibilidad total, la carga debe transportarse en C = K/3 diferentes tipos de PI-containers.
Proporcionamos modelos para cada uno de los cuatro casos explicados arriba. Los modelos permanecen iguales excepto por el valor de C (el número de grupos de compatibilidad) y los tipos de carga en cada grupo de compatibilidad. Después de llegar al hub principal en una región, los flujos dentro de esa región quedan fuera del alcance estratégico de nuestro modelo. Primero, definimos las notaciones usadas en el modelo de equilibrio de flujo:
Conjuntos
$$ H = \{1, \dots, N\}, \text{ conjunto de todos los hubs.} $$
$$ F = \{1, \dots, K\}, \text{ conjunto de todos los tipos de carga.} $$
$$ F^p \subset F = \text{ subconjunto } p \text{ de tipos de carga que son compatibles en términos de PI-containers } p = 1, \dots, C $$
Índices
$$ i, j \in H \text{ indica hubs regionales.} $$
$$ k \in F \text{ indica tipo de carga o PI-container.} $$
$$ p = 1, \dots, C \text{ indica un grupo de tipos de carga compatibles.} $$
Parámetros
$$ D_{jkp} \text{:} \text{ demanda en toneladas para PI-containers en el hub } j \text{ para el tipo de carga } k \in F^p \text{ para } p = 1, \dots, C $$
$$ S_{ikp} \text{:} \text{ oferta en toneladas para PI-containers en el hub } i \text{ para el tipo de carga } k \in F^p \text{ para } p = 1, \dots, C $$
Variables de decisión
$$ X_{pij} \text{:} \text{ el flujo en toneladas de carga desde el hub } i \text{ hacia } j \text{ para } p = 1, \dots, C \text{ (total para todos } k \in F^p\text{)} $$
$$ fb_{pij} \text{:} \text{ la diferencia en toneladas entre los flujos entre el hub } i \text{ hacia } j \text{ y el hub } j \text{ hacia } i \text{ para } p = 1, \dots, C \text{ (total para todos } k \in F^p\text{)} $$
La Figura 4 presenta el Modelo de red PIC. En el Modelo PIC, C ∈ {1, 4, 8, 12} indica la compatibilidad asumida. En este sentido, tenemos cuatro modelos equivalentes.
Modelo PIC
$$ \text{Min } \sum_{p=1}^{C} \sum_{i=1}^{N} \sum_{j=i+1}^{N} |fb_{pij}| \quad (1) $$
Sujeto a.
$$ \sum_{j=1}^{N} X_{pij} \leq \sum_{k \in F^p} S_{ikp} \text{ para todo } i \text{ y } p \in \{1, \dots, C\} \quad (2) $$
$$ \sum_{i=1}^{N} X_{pij} = \sum_{k \in F^p} D_{jkp} \text{ para todo } j \text{ y } p \in \{1, \dots, C\} \quad (3) $$
$$ fb_{pij} = X_{pij} - X_{pji} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ y } j = i+1, \dots, N \quad (4) $$
$$ X_{kij} \geq 0 \text{ para todo } k \in F^C \text{ y } i, j \in H \quad (5) $$
$$ fb_{kij} \text{ irrestricto } k \in F^C \text{ y } i, j \in H \quad (6) $$
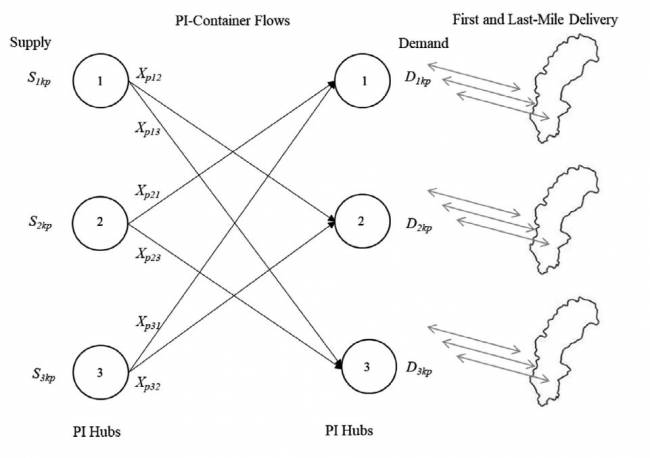
La función objetivo (1) del Modelo PIC calcula los desequilibrios totales de flujo entre los hubs de origen y destino. Cabe señalar que la función incluye una función de valor absoluto que hace que el modelo sea no lineal. Posteriormente linealizamos esta función añadiendo nuevas variables y restricciones al modelo (Apéndice A). En el conjunto de restricciones (2), aseguramos que los contenedores PI que van del hub j a los otros hubs no excedan la cantidad recibida en el hub j (ver Figura 4). En el conjunto de restricciones (3), garantizamos que el hub i reciba todos los contenedores PI que necesita (ver Figura 4). En los conjuntos de restricciones (2) y (3), consideramos cada grupo de compatibilidad, p, como una mercancía agregada y, por lo tanto, calculamos el suministro total y la demanda total para el grupo p sumando el suministro y la demanda de las mercancías de ese grupo. El valor máximo de p proviene de C, indicando cuántos grupos de compatibilidad hay en cada escenario. En el conjunto de restricciones (4), calculamos los desequilibrios de flujo para cada grupo de compatibilidad p entre cada hub.
Los contenedores PI deben ser reposicionados; por lo tanto, solo debemos calcular los desequilibrios en una dirección ya que serán los mismos en la dirección inversa. El conjunto de restricciones (5) asegura la no negatividad de los flujos, y el conjunto de restricciones (6) especifica que los desequilibrios son irrestrictos en cuanto al signo.
Para resolver el modelo como un programa lineal, la función objetivo debe ser linealizada añadiendo un nuevo conjunto de variables y restricciones al modelo, como se detalla en el Apéndice A.
Suposiciones
Esta sección discute las suposiciones subyacentes de nuestro artículo.
Suposición #1: Red logística híbrida
Dado el enorme nivel de inversiones y el tiempo necesario para construir los componentes del Internet Físico, las décadas de sistemas híbridos están en el futuro. Fazili et al. (2017) describen un sistema híbrido, es decir, el sistema logístico convencional coexistiendo con el Internet Físico. Por lo tanto, la suposición de un sistema híbrido es la más realista y la aplicada en este artículo. La implementación de dicha red logística híbrida asume que la frontera entre los sistemas logísticos convencional y PI puede ser el hub PI; es decir, las mercancías pueden descargarse en el hub PI y empacarse en los contenedores PI del hub. Dado su contexto estratégico (Bartolacci et al. 2012), este manuscrito describe el “PI” del sistema (transporte intrarregional terminal a terminal).
Suposición #2: Tasa de llenado del camión en rutas con desequilibrio
Con sus largas distancias, pueblos y aldeas rurales, el norte de Suecia se caracteriza por una colaboración horizontal significativa (descrita por, por ejemplo, Hagebäck y Segerstedt (2004)). Los dos mayores minoristas de alimentos, ICA y COOP, distribuyen conjuntamente a los minoristas de alimentos; y los proveedores de servicios logísticos Schenker y DHL colaboran. Esta colaboración está impulsada por la absoluta necesidad de maximizar las tasas de llenado, como se verificó en una entrevista con un gerente de distrito del norte (Experto 2). Aunque no se aplica con tanta fuerza, las rutas hacia áreas con alta demanda de bienes (por ejemplo, Estocolmo) están prácticamente llenas. Por lo tanto, los transportistas saben que es muy poco probable que consigan una carga de retorno y que tendrán que regresar vacíos (Expertos 3, 4 y 5).
Suposición #3: Peso y plegabilidad del embalaje
La carga general generalmente no son mercancías paletizadas, sino material de construcción y componentes, tambores, barriles, componentes de vehículos, etc., que representan los flujos de carga entre origen y destino—normalmente con diferentes tipos de carga yendo en las respectivas direcciones (Expertos 1 y 5 y conjunto de datos de carga). Suponemos, para nuestro modelo, que el peso del embalaje (y la capacidad) de la caja mediana m-box (400 × 600 × 400) representa todos los tipos de contenedores PI más pequeños o más grandes (o m-boxes y versiones futuras especializadas de m-boxes). Este supuesto no será cierto, ya que los contenedores PI específicos diseñados para uno o más tipos de mercancías tendrán un tamaño diferente al de la m-box; sin embargo, no afectará en gran medida los resultados (que examinan el efecto agregado en la red). Según Landschützer et al. (2018), una m-box regular pesa 4.5 kg. La m-box está diseñada en relación con el Euro-palé (base de 800 mm × 1200 mm); es decir, se pueden cargar 4 m-boxes por palé (base) y apilar 6 en alto. Dado que una combinación sueca regular es de 18 (camión) + 33 (remolque) palés, el peso del embalaje es 51 × 4 × 6 × 4.5 kg = 5508 kg (1224 contenedores PI (m-boxes) * 4.5 kg). En el transporte de carga general en Suecia, la restricción de volumen de la combinación vehicular suele ser el factor limitante más que el límite de peso[2]. Un camión lleno pesa 25 toneladas y puede albergar 1224 m-boxes. Por lo tanto, se asume que un contenedor PI representativo transporta 20.42 kg. Aunque las m-boxes actualmente no son plegables, asumimos que lo serán en versiones futuras (en los escenarios de flujos compatibles); de lo contrario, todo el Internet Físico se convierte en un sistema de un solo carril con contenedores PI llenos saliendo y vacíos regresando (especificidad de sinergia como se explica en el marco basado en la modularidad de servicio).
Suposición #4: Desequilibrios agregados
En la medida de nuestro conocimiento, los desequilibrios en los flujos entre origen y destino no han sido abordados en el contexto del PI (Sternberg y Norrman 2017). En contraste, nuestro modelo aborda esta cuestión a nivel agregado. No incluimos ninguna restricción operativa (por ejemplo, ventanas de tiempo, tiempos de espera, carga y descarga), que son críticas para la planificación a nivel operativo en PI; sin embargo, no son necesarias para determinar los efectos de los desequilibrios. Nuestro propósito no es proporcionar una solución detallada a un problema operativo del PI (c.f. Hauder et al. 2018), sino estudiar cómo los desequilibrios comerciales y la (in)compatibilidad de la carga pueden generar la necesidad de reposicionamiento de contenedores PI vacíos.
Suposición #5: Economía de la diversidad de productos
Una suposición subyacente es que la heterogeneidad de las demandas de los servicios de logística y transporte permanecerá constante; es decir, los clientes continuarán consumiendo una gran variedad de productos, es decir, economía de diversidad de productos (Suzuki y Lu 2017). Dados estos considerandos, las tasas de llenado proporcionadas por Wall (2013) y Pålsson y Sternberg (2018), y el peso de los contenedores PI, hemos utilizado 25 toneladas como el peso cuando se utiliza la capacidad máxima de volumen de una combinación de camiones (como se explicó anteriormente, es el volumen y no el peso lo que determina cuándo un camión que transporta carga general está lleno).
Suposición #6: Compatibilidad de los contenedores PI (categorías de carga)
Las 12 categorías de carga identificadas (SAMGODS) se transportan actualmente utilizando el mismo camión y sin un embalaje de transporte designado (aparte de los palés Euro). Para ilustrar esto en el contexto de diferentes tipos de carga que se dirigen en diferentes direcciones, véase la Figura 5.

Basándonos en consultas con expertos (particularmente el Experto 1), nuestra matriz de compatibilidad asume las siguientes propiedades:
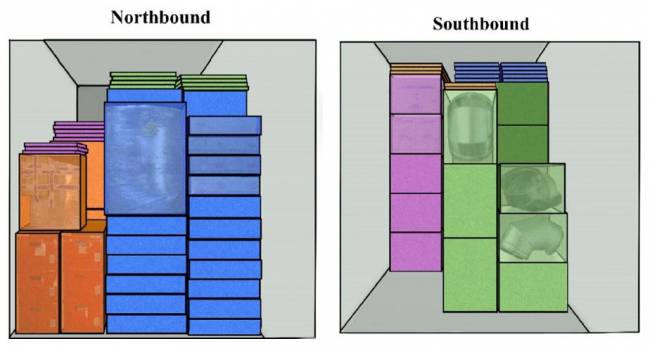
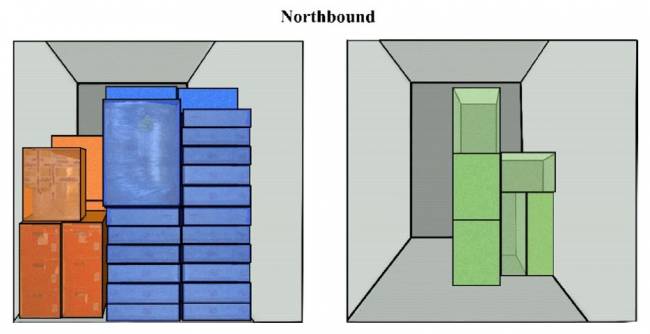
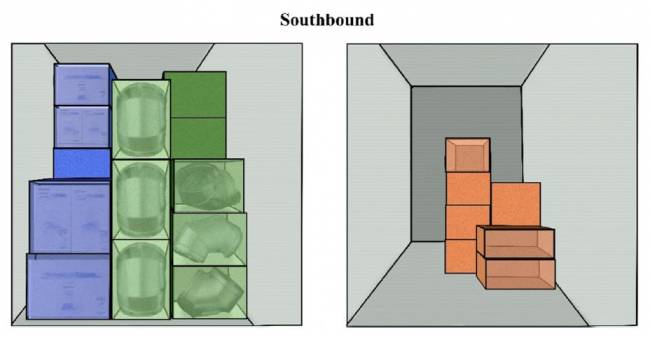
Compatibilidad total (Escenario 1): Este caso existe actualmente; es decir, diferentes tipos de carga general pueden transportarse en dos direcciones (carga que va entre dos puntos de enlace) utilizando el mismo vehículo (Experto 5). Lo ilustramos en la Figura 6.
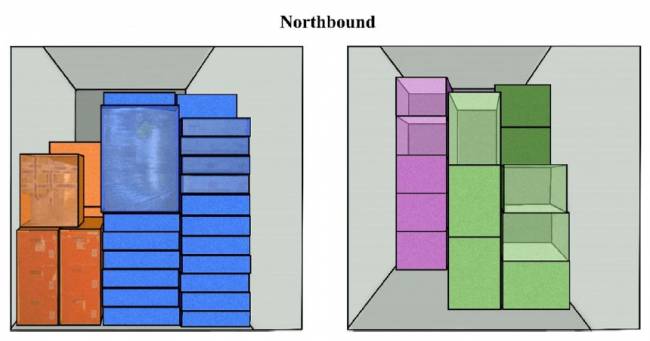
Sin compatibilidad (Escenario 2): Los contenedores PI altamente especializados impiden la integración entre envíos, ya que un efecto de los contenedores PI es ser altamente específicos para cada tipo de carga (ilustrado en la Figura 7).
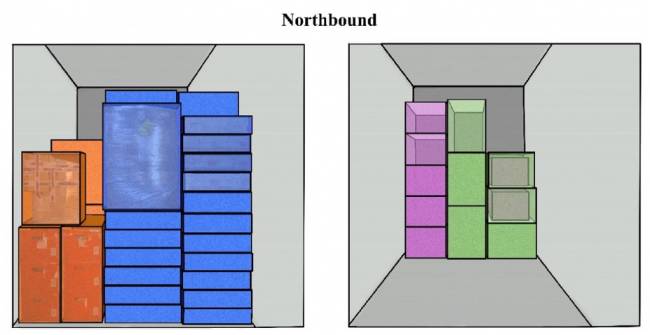
Compatibilidad limitada (Escenario 3): En este caso, asumimos que algunos de los tipos de carga más similares y fáciles de cargar son compatibles, mientras que otros no lo son, lo que genera la siguiente matriz:
En la Figura 8 y la Figura 9, ilustramos la compatibilidad limitada; es decir, más tipos, pero no todos, de carga pueden usar los mismos contenedores PI. Posteriormente, este escenario resultará en más reposicionamientos que en el Escenario 1 (compatibilidad total) pero significativamente menos que en el Escenario 2 (sin compatibilidad).
Alguna compatibilidad (Escenario 4): En este caso, alimentos, textiles y forraje pueden ir juntos; y madera, metal y papel son compatibles, generando lo siguiente:
Suposición #7: PI utiliza control centralizado; el sistema convencional no
El Escenario 1 representa la optimización de flujos en un escenario de contenedores PI completamente compatibles. Teóricamente, este escenario podría aplicarse al control centralizado de todos los flujos en una red logística convencional (es decir, agrupación tradicional de recursos sin implementar PI). Sin embargo, por ejemplo, Simmer et al. (2017) señalan que los actores no están dispuestos a ceder el control. Por lo tanto, el control centralizado en un sistema logístico convencional se considera poco realista (a menos que el entorno genere urgencia hacia ello, como en Hagebäck y Segerstedt (2004)). Los expertos 3 y 4 también enfatizaron fuertemente este punto. Por lo tanto, este manuscrito se enfoca únicamente en escenarios con PI implementado.
RESULTADOS
En esta sección, presentamos los resultados de los modelos utilizando datos de carga interregional de las diversas regiones norte, centro y sur de Suecia. Nuestro conjunto de datos contiene 12 tipos de carga transportados entre tres regiones principales (hubs).
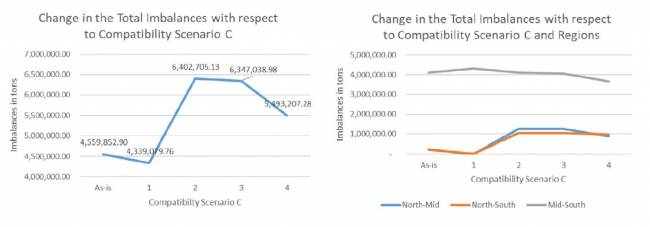
La Figura 10 presenta los resultados para los desequilibrios totales de todos los escenarios de compatibilidad comparados entre sí.
Como se observa en la Figura 10, la compatibilidad marca una diferencia significativa en los desequilibrios totales de flujo. En la práctica actual, la carga se transporta en pallets que pueden ser cargados en el mismo contenedor. Los desequilibrios son los segundos más bajos (tal como están) entre todos los escenarios, probablemente porque no hay una optimización centralizada. El valor optimizado (C = 1) es más bajo que el caso tal como está. El mayor desequilibrio se observa cuando los contenedores PI no son compatibles, C = 12. Los escenarios 2 y 3 para C = 8 y C = 4, respectivamente, siguen un patrón decreciente a medida que aumenta la compatibilidad.
En el gráfico derecho de la Figura 10, los desequilibrios están distribuidos entre las regiones. El desequilibrio entre las regiones sur y centro es el más alto. El comercio entre estas dos regiones representa la mayor parte en el país. Curiosamente, los resultados de la práctica tal como está y el escenario óptimo (C = 1) se invierten, con la práctica real conduciendo a un menor desequilibrio entre las regiones sur y centro, aunque el óptimo, C = 1, es el más bajo en todas las regiones, como se esperaba. Recuerde que la optimización involucra todas las regiones. Los resultados para cada escenario de compatibilidad son los siguientes: C = 1 representa modularidad de servicio sin cambios; y C = 4, C = 8 y C = 12 representan modularidad decreciente.
En el modelo de PL, usamos toneladas como unidad de transporte, por lo que la solución del modelo proporciona los desequilibrios entre diferentes regiones en toneladas. Sin embargo, puede interesar saber cuántos contenedores PI necesitan reposicionamiento. Si se conoce el tamaño del contenedor PI (cuánto peso de una categoría de producto transporta), basado en los desequilibrios en toneladas, se puede calcular el número de contenedores PI que necesitan reposicionamiento. Cabe señalar que cada grupo de compatibilidad puede estar asociado directamente con un tamaño diferente de contenedor PI. Esto no significa que no puedan usarse diferentes tamaños de contenedores PI para el mismo grupo de compatibilidad. En este caso, debemos asumir un tamaño promedio de contenedor PI si es necesario calcular el número de contenedores PI que deben ser reposicionados. Nuestro modelo de PL asume las mejores tasas de llenado y no impone una restricción al tamaño del contenedor PI. Si las tasas reales de llenado son menores, la necesidad de reposicionamiento de contenedores PI vacíos será mayor. En el Apéndice C, presentamos el número de contenedores PI que deben ser reposicionados bajo cada escenario basado en los desequilibrios totales presentados en la Figura 10.
Escenario 1: C = 1
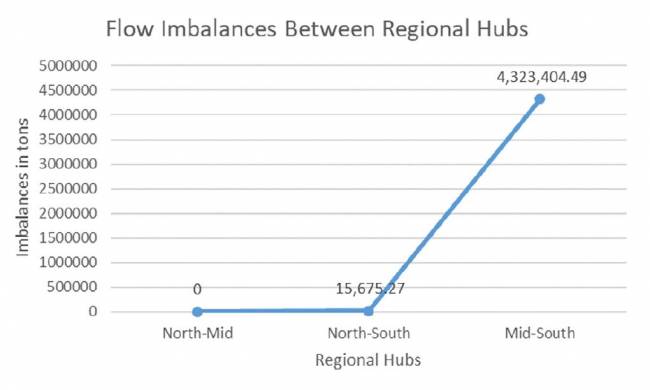
Cuando C = 1, asumimos que los contenedores PI son universalmente compatibles e intercambiables para todos los tipos de carga (como con la carga general actual). Abordando el Internet Físico como Montreuil (2011) lo propuso, este escenario de mejor caso puede agregar todos los flujos al calcular los desequilibrios de flujo. Nuestros resultados con datos interregionales de Suecia arrojan un desequilibrio total minimizado de 4,339,079.76 toneladas de carga (ver Figura 10), lo que equivale a 173,564 viajes de camión, cada uno transportando 25 toneladas de carga neta. Los desequilibrios entre los hubs regionales representan el 7.6% de la actividad total de transporte (de 57,157,318.12 toneladas); estos desequilibrios se muestran en el Apéndice B y se ofrece una representación gráfica en la Figura 11.
Una comparación de los desequilibrios minimizados (4,339,079.76 toneladas o 7.6%) y aquellos en los flujos reales (4,559,852.90 toneladas o 8%, calculados usando los datos de flujo real) refleja el potencial de mejora al usar la optimización para determinar los flujos entre los hubs PI.
Escenario 2: C = 12
En el Escenario 2, suponemos que no hay compatibilidad entre las cargas en términos de los contenedores PI, lo que significa que diferentes tipos de carga (ver Tabla 2) no pueden ser transportados en los mismos contenedores PI y que el servicio logístico se vuelve menos modularizado. Por lo tanto, es el escenario de peor caso. Nuestros resultados muestran que el desequilibrio total de flujo es de 6,402,705.13 toneladas (ver Figura 10), lo que se traduce en 256,109 camiones que pueden transportar 25 toneladas. La carga total transportada es de 57,157,318.12 toneladas. Por lo tanto, los desequilibrios representan el 11.2% de la actividad total de transporte. Los desequilibrios detallados entre los centros regionales se muestran en el Apéndice B, y una representación gráfica se proporciona en la Figura 12.
| Materia prima (tipo) | Incluido en este estudio |
|---|---|
| 1 Cereales (granel seco) | |
| 2 Patatas, otras verduras, frescas o congeladas, fruta fresca (granel seco) | X |
| 3 Animales vivos (granel seco) | |
| 4 Remolacha azucarera (granel seco) | |
| 5 Madera para la industria papelera (pasta de madera) (granel seco) | |
| 6 Madera aproximadamente cuadrada o aserrada en sentido longitudinal, cortada en láminas o pelada (granel seco) | X |
| 7 Astillas de madera y desechos de madera (granel seco) | |
| 8 Otra madera o corcho (granel seco) | No matriz PWC |
| 9 Textiles, artículos textiles y fibras sintéticas, otras materias primas animales y vegetales (carga general) | X |
| 10 Productos alimenticios y piensos para animales (carga general) | X |
| 11 Semillas oleaginosas y frutos oleaginosos y grasas (granel líquido) | |
| 12 Combustibles minerales sólidos (granel líquido) | |
| 13 Petróleo crudo (granel líquido) | |
| 14 Productos derivados del petróleo (granel líquido) | |
| 15 Mineral de hierro, desechos de hierro y acero y polvo de alto horno (granel seco) | |
| 16 Minerales y desechos no férricos (granel seco) | |
| 17 Productos metálicos (carga general) | X |
| 18 Cemento, cal, materiales de construcción manufacturados (granel seco) | |
| 19 Tierra, arena y grava (granel seco) | |
| 20 Otros minerales crudos y manufacturados (granel seco) | |
| 21 Fertilizantes naturales y químicos (granel seco) | |
| 22 Químicos del carbón (granel líquido) | |
| 23 Químicos distintos de los químicos del carbón y alquitrán (granel seco) | X |
| 24 Pulpa de papel y papel usado (granel seco) | |
| 25 Equipos de transporte, ensamblados o no, y partes de ellos (carga general) | X |
| 26 Manufacturas de metal (carga general) | X |
| 27 Vidrio, cristalería, productos cerámicos (carga general) | X |
| 28 Papel, cartón; no manufacturado (granel seco) | |
| 29 Cuero, textiles, ropa, otros artículos manufacturados que no sean papel, cartón y sus manufacturas (carga general) | X |
| 30 Cargas mixtas y parciales, artículos misceláneos (carga general) | No matriz PWC |
| 31 Madera para aserradero (granel seco) | |
| 32 Maquinaria, aparatos, motores, ensamblados o no, y partes de ellos (carga general) | X |
| 33 Papel, cartón y sus manufacturas (carga general) | X |
| 34 Material de embalaje utilizado (granel seco) | No matriz PWC |
| 35 Carga aérea (carga general) |
Escenario 3: C = 8
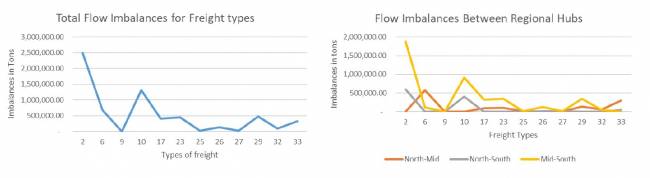
En el Escenario 3, asumimos una compatibilidad parcial entre los tipos de carga mostrados en la Tabla 3. Tenemos ocho grupos de carga; los tipos de carga en cada grupo son compatibles entre sí y pueden compartir los mismos contenedores PI. Nuestros resultados muestran que el desequilibrio total del flujo es de 6, 347,038.98 toneladas (ver Figura 10), lo que se traduce en 253,882 camiones que pueden transportar 25 toneladas. La carga total transportada es de 57,157,318.12 toneladas. Por lo tanto, los desequilibrios representan el 11.1% de la actividad total de transporte, no significativamente diferente del Escenario 2. Reducir a 8 grupos compatibles desde 12 (escenario sin compatibilidad) no tuvo un gran impacto. Los desequilibrios detallados entre los centros regionales se muestran en el Apéndice B, y se proporciona una representación gráfica en la Figura 13.
| Categorías | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Tipos de carga | 2, 10 | 9, 29 | 6 | 17 | 23 | 25, 26 | 27, 32 | 33 |
Escenario 4: C = 4
En el Escenario 4, asumimos que hay más tipos de carga compatibles que en el Escenario 3. Según la agrupación en la Tabla 4, tenemos cuatro grupos de carga de modo que los tipos en cada grupo son compatibles entre sí y pueden compartir los mismos contenedores PI. En este caso, los desequilibrios totales son de 5,493,207.28 toneladas (ver Figura 10) y 219,728 camiones de 25 toneladas. Estos desequilibrios representan el 10% de la carga total. A medida que la carga se vuelve progresivamente más compatible con los contenedores PI, los desequilibrios disminuyen. Sin embargo, el mínimo en el Escenario 1 corresponde al 7.6% de todos los transportes de carga en Suecia, lo que sugiere que los desequilibrios entre las regiones en términos de oferta y demanda para diferentes tipos de mercancías todavía requerirán flujos inversos de contenedores vacíos, representando el 7.6% de la actividad logística total en las carreteras. Los desequilibrios detallados entre hubs regionales se muestran en el Apéndice B, y una representación gráfica se proporciona en la Figura 14.
| Categorías | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Tipos de carga | 2, 9, 10, 29 | 6, 17, 26, 33 | 23 | 25, 27, 32 |
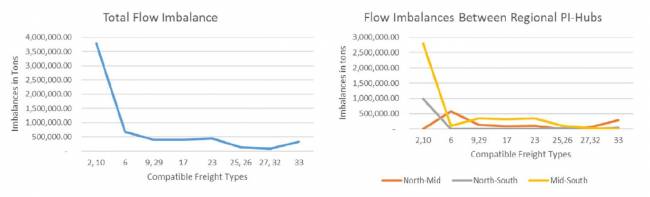
Como se muestra en las Figuras 13-15, los desequilibrios más altos son para tipos de carga o grupos de compatibilidad que incluyen los alimentos 2 y 10. Nuevamente, los desequilibrios más altos están entre las regiones sur y media (Figura 15).
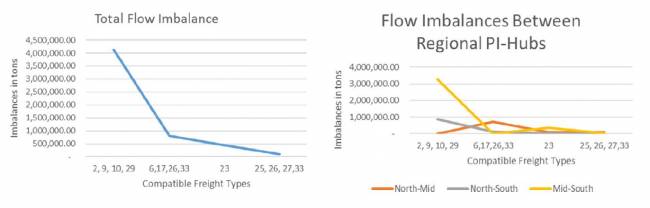
Para determinar si los cambios en los datos de entrada afectan los resultados, también realizamos un análisis de sensibilidad considerando las siguientes modificaciones en la demanda para diferentes cargas y regiones:
• La demanda en los tres centros (sur, medio y norte) se redujo en un 10%, 7,5% y 5%, respectivamente (considerando la sensibilidad general del modelo).
• No hubo reducción para los tipos de flete 2 y 10 (alimentos), reducción del 10% en todos los demás tipos.
• La demanda en los tres centros (sur, medio y norte) aumentó en un 10%, 7,5% y 5%, respectivamente (considerando la sensibilidad general del modelo).
Los datos originales se obtuvieron bajo condiciones económicas regulares. Asumimos que la demanda puede aumentar (auge económico) o disminuir (recesión económica). En consecuencia, primero consideramos el caso en que la demanda disminuye en todas las regiones en ciertas proporciones basadas en los bienes demandados en esas regiones. En segundo lugar, asumiendo que la demanda de alimentos permanece igual incluso durante una recesión, consideramos reducciones de demanda para todos los artículos que no sean alimentos. En tercer lugar, consideramos el caso en que la demanda aumenta debido a un auge económico. Por razones de espacio, los resultados de estas suposiciones se pueden encontrar en el Apéndice D.
IMPLICACIONES Y DISCUSIÓN
En respuesta a varios llamados a la investigación, este estudio ha analizado el Internet Físico utilizando datos empíricos y suposiciones realistas basadas en aportes de la literatura y expertos de la industria. Nos hemos centrado en analizar los efectos potenciales de diferentes niveles de heterogeneidad de las entradas, determinados por la compatibilidad de los contenedores PI. Nuestro análisis revela un desequilibrio en el mejor de los casos del 7,6%, lo que representa una mejora en comparación con los desequilibrios del sistema logístico convencional actual. Si se puede mantener la compatibilidad del embalaje entre los contenedores PI (como en el Escenario 1) y si se pueden aprovechar los beneficios de la automatización en las terminales habilitados por los contenedores PI, la especificidad sinérgica será baja. Además, la urgencia de los principales interesados para promover la modularización a través del Internet Físico aumentará, porque PI será uno de los facilitadores tecnológicos, operacionalizando la optimización. En el mejor de los casos (Escenario 1), PI representa una visión deseable de las cadenas de suministro futuras.
El desequilibrio del mejor escenario (7,6%) debe compararse con el 11,2% y 11,1% de desequilibrios en los escenarios donde los contenedores PI carecen de compatibilidad (Escenarios 2 y 3, respectivamente). La falta de compatibilidad entre los contenedores PI causará especificidad sinérgica contra la modularización e implementación del Internet Físico porque el concepto podría fallar en mejorar las tasas de llenado. En comparación con el Escenario 1, el Escenario 2 representa 82.545 cargas de camión adicionales por año entre las regiones norte y sur, lo que representa un costo extra sustancial para los embarcadores y un impacto ambiental logístico negativo aumentado. Curiosamente, los Escenarios 2 y 3 difieren poco en cuanto al efecto sobre los volúmenes totales de carga. Sin embargo, a medida que la heterogeneidad relativa de las entradas disminuye en el Escenario 4, el desequilibrio total disminuye al 10%.
Crítica e investigación futura
Nuestro análisis se ha basado en siete suposiciones, incluida la que las demandas heterogéneas de los servicios logísticos permanecerán constantes. Sin embargo, se recomienda que la investigación futura evalúe la validez de esa suposición, así como de las demás, mediante ensayos piloto de Internet Físico, múltiples estudios de caso o investigaciones basadas en encuestas.
El modelo matemático que hemos presentado en este artículo aborda el problema de reposicionamiento de contenedores PI a nivel estratégico y agregado entre los PI-hubs. Debido a su naturaleza estratégica, este artículo no incorpora los detalles operativos del problema (por ejemplo, cómo se cargan los contenedores PI con mercancías para minimizar el número de contenedores PI necesarios, cómo se cargan los contenedores de transporte con los contenedores PI, el tiempo para cargar/descargar los contenedores PI en los contenedores de transporte y los contenedores de transporte en los camiones, y cómo se enrutann los camiones entre los PI-hubs). Incluir estos detalles permitiría que el modelo proporcione soluciones para otros problemas operativos en el PI. Los modelos disponibles en la literatura tradicional de reposicionamiento marítimo de contenedores pueden ser la base para desarrollar modelos que incorporen las nuevas características del reposicionamiento de contenedores PI. Dichos modelos no solo serán de gran tamaño debido a la introducción de nuevas variables y restricciones para abordar los detalles mencionados anteriormente del problema, sino también más difíciles de resolver, especialmente cuando se involucran variables enteras/binarias típicas en dicho modelado. Estos factores enfatizarán la necesidad de desarrollar procedimientos de solución eficientes que puedan resolver tales modelos destinados a la planificación central del PI a diario. Dichos modelos podrían potencialmente incluir problemas de primera y última milla y la relación con la logística colaborativa (Carbone et al. 2017; Castillo et al. 2018). Chen y Pan (2015) y Rai et al. (2017) han sugerido investigar el PI como una forma de gestionar la logística colaborativa.
Este artículo ilustra la importancia de continuar investigando sobre los contenedores PI, teniendo en cuenta la teoría de la modularidad y la heterogeneidad de los insumos. Los futuros proyectos de investigación deben intensificar los esfuerzos de diseño para los contenedores PI si el Internet Físico quiere mantener su posición como una visión sostenible de la logística futura. Proponemos una investigación interdisciplinaria de ciencia del diseño para abordar esta brecha urgente de investigación y desarrollo. Además, tales esfuerzos de investigación deben abordar la compatibilidad entre continentes, ya que un sistema logístico diseñado solo para el mercado europeo podría aumentar las ineficiencias en el transporte internacional. Dada la importancia del sistema de embalaje, se necesita investigación sobre cómo podría adoptarse un sistema de embalaje a nivel industrial (por ejemplo, estudiando los sistemas secundarios de embalaje a nivel industrial que se han adoptado a lo largo de Escandinavia).
Implicaciones teóricas
Este artículo contribuye a la teoría de rango medio de la modularización contextualizada del servicio logístico (de Blok et al. 2014; Brax et al. 2017) al analizar los efectos estratégicos de la modularización en el Internet Físico. También contribuye a la literatura creciente sobre el Internet Físico al mostrar la aplicabilidad y utilidad de operacionalizar la teoría de la modularidad aplicada a servicios logísticos. Basándonos en el modelado matemático y la teoría de la modularidad, nuestros hallazgos enfatizan la importancia de la modularización del servicio logístico sin aumentar la heterogeneidad de los insumos.
La investigación sobre el Internet Físico está aún en sus inicios, y queda mucho trabajo por hacer. Nuestro análisis, así como las futuras direcciones de investigación que proponemos, destaca la importancia de considerar el diseño del embalaje en la modularización de la logística y el transporte, y aún más en el contexto del Internet Físico.
Los hallazgos muestran que si los componentes están bien diseñados, el Internet Físico puede potencialmente reducir los desequilibrios mediante la optimización de los flujos de carga y la reposición de contenedores PI. Sin embargo, también puede aumentar los desequilibrios. El PI es esencialmente modularización, pero paradójicamente puede resultar en una menor compatibilidad de los servicios logísticos si los contenedores PI no están bien diseñados. Esta paradoja debe ser considerada en futuras investigaciones sobre los efectos del Internet Físico.
Implicaciones prácticas
Para que el Internet Físico se convierta en una realidad, serán necesarias grandes inversiones tanto por parte de actores públicos como privados. Nuestro modelo presenta una herramienta valiosa para los responsables políticos en la evaluación de los beneficios de la implementación del PI. Además, hacemos una contribución significativa en la orientación de las agencias financiadoras sobre temas del PI vitales para su futura implementación.
Se recuerda a los responsables políticos su papel en crear la urgencia necesaria para promover la modularización. Se aconseja a la Comisión Europea que impulsar políticas que disminuyan la urgencia de modularizar (al promover estrategias que faciliten el uso extensivo de transportistas de bajo costo) y simultáneamente invertir en la implementación del Internet Físico probablemente no producirá los efectos deseados, comparable a cómo la producción de bajo costo evitó la modularización a gran escala en la fabricación (Starr 2010).
Mediante el uso de los conocimientos de nuestra investigación, los profesionales deberían poder tener una visión objetiva de los posibles efectos de los contenedores PI en su cadena de suministro. Como se ejemplifica en nuestros análisis, la adopción de contenedores PI puede tener un impacto positivo o negativo en los balances de carga, dependiendo del diseño del contenedor PI.
El PI representa ganancias significativas de eficiencia, pero cualquier nuevo sistema de embalaje implica una compensación para los gerentes. La adopción de un embalaje que habilite la automatización podría ser beneficiosa a menos que las ganancias se vean compensadas por el costoso reposicionamiento del embalaje. Se aconseja a los gerentes seguir de cerca el desarrollo del PI y, específicamente, la compatibilidad del sistema de contenedores PI propuesto debido a su efecto en la eficiencia.
[1] ALICE es el acrónimo de Alliance for Logistics Innovation through Collaboration in Europe, una organización de lobby formada para desarrollar una estrategia para la investigación, innovación y despliegue en el mercado de la innovación en gestión de la cadena de suministro europea. Entre sus miembros se encuentran grandes corporaciones como Ford, Proctor & Gamble, Daimler y Volvo; actores públicos como las Correos Nacionales de Italia y el Puerto de Barcelona; y numerosos institutos de investigación como Mines ParisTech, Fraunhofer y RISE (https://www.etp-logistics.eu/?page_id=29).
[2] Esto es de acuerdo con los Expertos 3, 4, 5 y 6, así como en numerosos estudios sobre pesos promedio (Wall 2013). La excepción (cuando el peso es la restricción en lugar del volumen) suele ser las materias primas (Pålsson y Sternberg 2018).
APÉNDICE A
LINEALIZACIÓN DEL MODELO PIC
Para linearizar la función objetivo en el Modelo PI, definimos las siguientes variables técnicas y restricciones.
Definimos un conjunto de variables técnicas como
$$ t_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ y } j = i+1, \dots, N $$
Agregamos las siguientes restricciones para reemplazar la restricción (4) en PI:
$$ t_{pij} \geq fb_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ y } j = i+1, \dots, N $$
$$ t_{pij} \geq -fb_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ y } j = i+1, \dots, N $$
Tenga en cuenta que, dado que tpij son variables técnicas, no existe una definición en términos de las características del problema. El modelo linealizado PIC-L puede entonces formularse como
PIC-L
$$ \text{Min } \sum_{p=1}^{C} \sum_{i=1}^{N} \sum_{j=i+1}^{N} t_{pij} $$
sujeto a
$$ \sum_{j=1}^{N} X_{pij} \leq \sum_{k \in F^p} S_{ikp} \text{ para todo } i \text{ y } p \in \{1, \dots, C\} $$
$$ \sum_{i=1}^{N} X_{pij} = \sum_{k \in F^p} D_{jkp} \text{ para todo } j \text{ y } p \in \{1, \dots, C\} $$
$$ t_{pij} \geq fb_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ y } j = i+1, \dots, N $$
$$ t_{pij} \geq -fb_{pij} \text{ para todo } p \in \{1, \dots, C\}, i \in H, \text{ y } j = i+1, \dots, N $$
$$ X_{kij} \geq 0 \text{ para todo } k \in F^C \text{ y } i, j \in H $$
$$ fb_{kij} \text{ sin restricciones } k \in F^C \text{ y } i, j \in H $$
Tenga en cuenta que usamos PIC-L en nuestros experimentos.
APÉNDICE B
Este apéndice proporciona los resultados con más detalle para los desequilibrios totales de flujo de los cuatro escenarios que simulamos utilizando nuestro modelo matemático. Los números entre paréntesis son los negativos del desequilibrio en la dirección opuesta. Por ejemplo, en la Tabla B1 el desequilibrio entre norte y sur es 15,675.27, indicando que el norte envía esa cantidad de carga (en toneladas) más al sur. Por lo tanto, el desequilibrio entre sur y norte es -15,675.27, indicando que el sur envía esa cantidad de carga (en toneladas) menos al norte.
Tabla B1: Desequilibrios de flujo entre los centros regionales en Suecia para el Escenario 1 C = 1
| De/Hacia | Norte | Medio | Sur |
|---|---|---|---|
| Norte | – | – | 15,675.27 |
| Medio | – | – | 4,323,404.49 |
| Sur | (15,675.27) | (4,323,404.49) | – |
Tabla B2: Desequilibrios de flujo entre los centros regionales en Suecia para el Escenario 2 C = 12
94| Tipo de carga | De/A | Norte | Medio | Sur |
|---|---|---|---|---|
| 2 | Norte | – | – | 593,224.25 |
| Medio | – | – | 1,887,794.49 | |
| Sur | (593,224.25) | (1,887,794.49) | – | |
| 6 | Norte | – | (577,627.15) | – |
| Medio | 577,627.15 | – | 106,659.86 | |
| Sur | – | (106,659.86) | – | |
| 9 | Norte | – | – | 15. |
| Centro | – | – | 5.06 | |
| Sur | (15.94) | (5.06) | – | |
| 10 | Norte | – | – | 396,501.19 |
| Centro | – | – | 914,356.22 | |
| Sur | (396,501.19) | (914,356.22) | – | |
| 17 | Norte | – | 84,064.81 | – |
| Centro | (84,064.81) | – | (317,317.87) | |
| Sur | – | 317,317.87 | – | |
| 23 | Norte | – | (99,093.37) | – |
| Centro | (99,093.37) | – | 345,368.23 | |
| Sur | – | (345,368.23) | – | |
| 25 | Norte | – | 12,148.84 | – |
| Medio | (12,148.84) | – | (5,328.56) | |
| Sur | – | 5,328.56 | – | |
| 26 | Norte | – | – | 12,500.91 |
| Medio | – | – | 125,393.69 | |
| Sur | (12,500.91) | (125,393.69) | – | |
| 27 | Norte | – | – | 9,248.68 |
| Medio | – | – | 11,797.78 | |
| Sur | (9,248.68) | (11,797.78) | – | |
| 29 | Norte | – | (134,150.75) | – |
| Medio | 134,150.75 | – | 341,745.08 | |
| Sur | – | (341,745.08) | – | |
| 32 | Norte | – | 50,500.36 | – |
| Medio | (50,500.36) | – | (46,203.59) | |
| Sur | – | 46,203.59 | – | |
| 33 | Norte | – | (294,976.84) | (36,681.61) |
| Medio | 294,976.84 | – | – | |
| Sur | 36,681.61 | – | – | |
Tabla B3: Desequilibrios de flujo entre centros regionales en Suecia para el Escenario 3 C = 8
| Tipo de carga | Desde/Hasta | Norte | Centro | Sur |
|---|---|---|---|---|
| 2, 10 | Norte | – | – | 989,725.44 |
| Centro | – | – | 2,802,150.71 | |
| Sur | (989,725.44) | (2,802,150.71) | – | |
| 6 | Norte | – | (577,627.15) | – |
| Centro | 577,627.15 | – | 106,659.86 | |
| Sur | – | (106,659.86) | – | |
| 9, 29 | Norte | – | (134,134.81) | – |
| Centro | 134,134.81 | – | 341,766.08 | |
| Sur | – | (341,766.08) | – | |
| 17 | Norte | – | 84,064.81 | – |
| Centro | (84,064.81) | – | (317,317.87) | |
| Sur | – | 317,317.87 | – | |
| 23 | Norte | – | (99,093.37) | – |
| Centro | 99,093.37 | – | 345,368.23 | |
| Sur | – | (345,368.23) | – | |
| 25, 26 | Norte | – | – | 24,649.75 |
| Centro | – | – | 107,916.28 | |
| Sur | (24,649.75) | (107,916.28) | – | |
| 27, 32 | Norte | – | 59,749.04 | – |
| Medio | (59,749.04) | – | (25,157.13) | |
| Sur | – | 25,157.13 | – | |
| 33 | Norte | – | (294,976.84) | (36,681.61) |
| Medio | 294,976.84 | – | – | |
| Sur | 36,681.61 | – | – | |
Tabla B4: Desequilibrios de flujo entre los centros regionales en Suecia para el Escenario 4 C = 4
| Tipo de carga | De/Hacia | Norte | Centro | Sur |
|---|---|---|---|---|
| 2, 9, 10, 29 | Norte | – | – | 855,590.63 |
| Centro | – | – | 3,278,051.60 | |
| Sur | (855,590.63) | (3,278,051.60) | – | |
| 6, 17, 26, 33 | Norte | – | (703,274.86) | (109,445.02) |
| Centro | 703,274.86 | – | – | |
| Sur | 109,445.02 | – | – | |
| 23 | Norte | – | (99,093.37) | – |
| Centro | 99,093.37 | – | 345,368.23 | |
| Sur | – | (345,368.23) | – | |
| 25, 27, 32 | Norte | – | – | 24,649.75 |
| Centro | – | – | 107,916.28 | |
| Sur | (24,649.75) | (107,916.28) | – | |
APÉNDICE C
Presentamos el número de contenedores PI que deben ser reposicionados basándonos en la suposición de que cada contenedor PI transporta 20,42 kg y pesa 4,5 kg, como se describe en la Suposición 3 del texto principal.
Tabla C1: Desbalances totales en toneladas entre regiones para cada uno de los diferentes escenarios (Tal cual, 1, 2, 3 y 4)
| Escenarios de Compatibilidad | ||||||
|---|---|---|---|---|---|---|
| Regiones | Tal cual | 1 | 2 | 3 | 4 | |
| Norte–medio | 220,773.15 | – | 1,252,562.11 | 1,249,646.01 | 874,266.11 | |
| Norte–sur | 236,448.42 | 15,675.27 | 1,048,172.59 | 1,051,056.80 | 965,035.65 | |
| Medio–sur | 4,102,631.34 | 4,323,404.49 | 4,101,970.43 | 4,046,336.16 | 3,653,905.52 | |
Tabla C2: Número de contenedores PI a reposicionar basado en los desequilibrios dados en la Tabla C1, y suponiendo que un contenedor PI transporta 20.42 kg de carga
| Regiones | Escenarios de compatibilidad | ||||
|---|---|---|---|---|---|
| Tal como está | 1 | 2 | 3 | 4 | |
| Norte–medio | 10,811,613.5 | – | 61,339,966.2 | 61,197,160.3 | 42,814,207.4 |
| Norte–sur | 11,579,256.4 | 767,642.9 | 51,330,684.9 | 51,471,929.6 | 47,259,336.5 |
| Medio–sur | 200,912,406.5 | 211,724,020.0 | 200,880,040.8 | 198,155,541.7 | 178,937,586.6 |
Tabla C3: Peso total (en toneladas) de contenedores vacíos que se deben reposicionar dado el número de contenedores PI en la Tabla C2 y asumiendo que un contenedor PI pesa 4.5 kg
| Regiones | Escenarios de Compatibilidad | ||||
|---|---|---|---|---|---|
| Como está | 1 | 2 | 3 | 4 | |
| Norte–medio | 48,652.3 | – | 276,029.8 | 275,387.2 | 192,663.9 |
| Norte–sur | 52,106.7 | 3,454.4 | 230,988.1 | 231,623.7 | 212,667.0 |
| Medio–sur | 904,105.8 | 952,758.1 | 903,960.2 | 891,699.9 | 805,219.1 |
APÉNDICE D
Realizamos un análisis de sensibilidad para determinar si los patrones que observamos cambiarían si hubiera cambios en la demanda. Los datos originales se obtuvieron bajo condiciones económicas regulares. Supusimos que la demanda podría disminuir durante las recesiones económicas. En consecuencia, primero consideramos el caso en el que la demanda disminuye en todas las regiones en ciertas proporciones basadas en los bienes demandados en esas regiones. En segundo lugar, asumiendo que la demanda de productos alimenticios se mantiene igual incluso durante una recesión, consideramos reducciones en la demanda para todos los productos excepto los alimentos. En tercer lugar, consideramos el caso en que la demanda aumenta debido a un auge económico. El aumento o disminución específica de la demanda que consideramos es la siguiente:
• La demanda en los tres hubs (sur, medio y norte) se redujo en un 10%, 7.5% y 5%, respectivamente (considerando la sensibilidad general del modelo).
• No hubo reducción para los tipos de carga 2 y 10 (alimentos), reducción del 10% en todos los demás tipos.
• La demanda en los tres centros (sur, medio y norte) aumentó en un 10%, 7,5% y 5%, respectivamente (considerando la sensibilidad general del modelo). Los resultados con demanda modificada muestran patrones muy similares a los resultados con demanda original en los tres casos, como se muestra en las Figuras D1–D3.
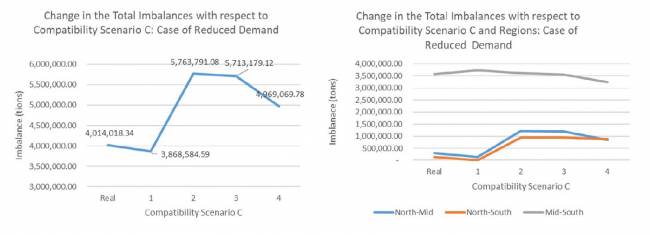
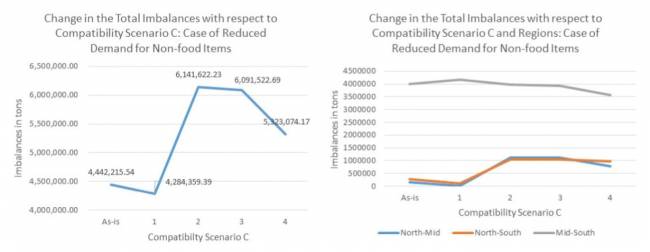
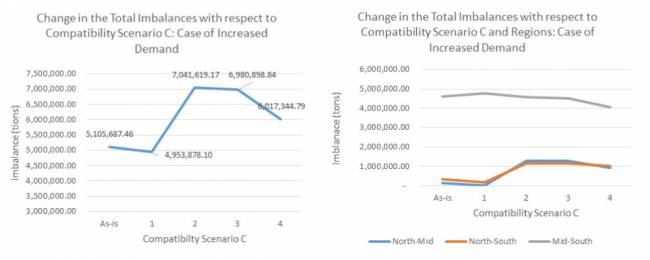
AUTORES
Henrik S. Sternberg (PhD, Chalmers University of Technology, Suecia) es Profesor Asistente de Gestión de la Cadena de Suministro en Ivy College of Business, Iowa State University. Sus intereses de investigación son la transparencia en la cadena de suministro, política de transporte, eficiencia logística, adopción de tecnología y crowdsourcing en la gestión de operaciones. La investigación del Dr. Sternberg está publicada, por ejemplo, en Journal of Business Logistics, International Journal of Physical Distribution & Logistics Management, International Journal of Logistics Management y Transportation Journal.
Meltem Denizel (PhD, Warrington School of Business, University of Florida) es Profesora Asociada de Gestión de la Cadena de Suministro en Ivy College of Business, Iowa State University. Sus intereses de investigación son las operaciones sostenibles, la eficiencia de la cadena de suministro, el modelado matemático y el dimensionamiento de lotes de producción. La investigación de la Dra. Denizel está publicada, por ejemplo, en Production and Operations Management, Operations Research, Decision Sciences, IIE Transactions, Transportation Journal y International Journal of Production Economics.
REFERENCIAS
ALICE2019. "Alliance for Logistics Innovation through Collaboration in Europe." ENIDE, accessed 25th of April. http://www.etp-logistics.eu/
Ambra, T., Caris, A., and Macharis, C. 2019. “Towards Freight Transport System Unification: Reviewing and Combining the Advancements in the Physical Internet and Synchromodal Transport Research.” International Journal of Production Research 57(6):1606–23.
Ambra, T., Caris, A., and Macharis, C. 2020. “Do You See What I See? A Simulation Analysis of Order Bundling within a Transparent User Network in Geographic Space.” Journal of Business Logistics Forthcoming 1–24. https://onlinelibrary. wiley.com/doi/10.1111/jbl.12237
Ballot, E., Bierlaire, M., Crainic, T.G., De Koster, R., Ellis, K.P., Fontane, F., Gendreault, M., Glardon, R., Gue, K.R., Hakimi, D., Heni, H., Labarthe, O., Lounes, M., Meller, R.D., Montreuil, B., Ogle, M., Smith, J., Shorabi, H., Th´emans, M., and Wieser, P. 2016. "The Physical Internet initiative." Mines ParisTech, accessed 2nd of January. http://www.physicalinte rnetinitiative.org/
Ballot, E., Gobet, O., and Montreuil, B. 2012. "Physical Internet Enabled Open Hub Network Design for Distributed Networked Operations." In Service Orientation in Holonic and Multi-Agent Manufacturing Control, edited by T. Borangiu, A. Thomas, and D. Trentesaux, 279–292. Warsaw, Poland: Springer.
Ballot, E., Montreuil, B., and Meller, R.D. 2014. The Physical Internet – The Network of Logistics Networks. Paris, France: La documentation Française. Ballot, E., Montreuil, B., and Thivierge, C. 2013. Functional Design of Physical Internet Facilities: A Road-Rail Hub. Montreal, Canada: CIRRELT.
Bartolacci, M.R., LeBlanc, L.J., Kayikci, Y., and Grossman, T.A. 2012. “Optimization Modeling for Logistics: Options and Implementations.” Journal of Business Logistics 33 (2):118–27.
Bergquist, M., Bernhardsson, V., and Rosklint, E. 2016. Representation of the Swedish Transport and Logistics System in Samgods v. 1.1. Linköping, Sweden: VTI.
Brax, S.A., Bask, A., Hsuan, J., and Voss, C.A. 2017. “Service Modularity and Architecture – An Overview and Research Agenda.” International Journal of Operations & Production Management 37(6):686–702.
Carbone, V., Rouquet, A., and Roussat, C. 2017. “The Rise of Crowd Logistics: A New Way to Co-Create Logistics Value.” Journal of Business Logistics 38(4):238–52.
Castillo, V.E., Bell, J.E., Rose, W.J., and Rodrigues, A.M. 2018. “Crowdsourcing Last Mile Delivery: Strategic Implications and Future Research Directions.” Journal of Business Logistics 39(1):7–25.
Chen, C., and Pan, S. 2015. "Using the Crowd of Taxis to Last Mile Delivery in E-commerce: A Methodological Research." SOHOMA’15, Cambridge, UK. CO3 Project. 2014. "CO3." NDL/HIDC, accessed October 11th. http://www.co3-project.eu/
Creemers, S., Woumans, G., Boute, R., and Beliën, J. 2017. “Tri-Vizor Uses an Efficient Algorithm to Identify Physical Internet—Logistics Service Modularity 159 Collaborative Shipping Opportunities.” Interfaces 47 (3):244–59.
de Blok, C., Meijboom, B., Luijkx, K., Schols, J., and Schroeder, R. 2014. “Interfaces in Service Modularity: A Typology Developed in Modular Health Care Provision.” Journal of Operations Management 32(4):175–89.
European Commission. 2016. Report from the Commission to the European Parliament and the Council. In COM (2016). Brussels, Belgium: European Commission.
Fazili, M., Venkatadri, U., Cyrus, P., and Tajbaksh, M. 2017. “Physical Internet, Conventional and Hybrid Logistic Systems: A Routing Optimisation-Based Comparison Using the Eastern Canada Road Network Case Study.” International Journal of Production Research 55(9):2703–30.
Hagebäck, C., and Segerstedt, A. 2004. “The Need for Co- Distribution in Rural Areas—A Study of Pajala in Sweden.” International Journal of Production Economics 89(2):153–63.
Hauder, V.A., Pitzer, E., and Affenzeller, M. 2018. “Optimization Approaches for the Physical Internet.” Lecture Notes in Computer Science 10697:236–45.
Hellström, D., and Nilsson, F. 2011. “Logistics-driven Packaging Innovation: A Case Study at IKEA.” International Journal of Retail and Distribution Management 39(9):638–57. Hesse, M., and Rodrigue, J.-P. 2004. “The Transport Geography of Logistics and Freight Distribution.” Journal of Transport Geography 12(3):171–84.
Hübner, A., and Ostermeier, M. 2019. “A Multi-Compartment Vehicle Routing Problem with Loading and Unloading Costs.” Transportation Science 53(1):282–300.
Jensen, A.F., Thorhauge, M., de Jong, G., Rich, J., Dekker, T., Johnson, D., Cabral, M.O., and Nielsen, O.A. 2019. “A Disaggregate Freight Transport Chain Choice Model for Europe.” Transportation Research Part E: Logistics and Transportation Review 121:43–62.
Jula, H., Chassiakos, A., and Ioannou, P. 2006. “Port Dynamic Empty Container Reuse.” Transportation Research Part E: Logistics and Transportation Review 42(1):43–60. Karlsson, R., and Bernhardsson, V. 2018. Calibration Report. Linköping, Sweden: VTI.
Kolar, P., Schramm, H.-J., and Prockl, G. 2018. “Intermodal Transport and Repositioning of Empty Containers in Central and Eastern Europe Hinterland.” Journal of Transport Geography 69:73–82.
Kuzmicz, K.A., and Pesch, E. 2019. “Approaches to Empty Container Repositioning Problems in the Context of Eurasian Intermodal Transportation.” Omega 85:194–213.
Landschutzer, C., Ehrentraut, F., and Jodin, D. 2015. “Containers for the Physical Internet: Requirements and Engineering Design Related to FMCG Logistics.” Logistics Research 8(8):1–22.
Landschützer, C., Jodin, D., and Ehrentraut, F. 2018. "Modular Boxes for the Physical Internet." Austria: Graz University of Technology, accessed October 14th. https://online.tugraz.a t/tug_online/voe_main2.getVollText?pDocumentNr= 901117&pCurrPk=81478
Ljungberg, A. 2013. “Impacts of Increased Rail Infrastructure Charges in Sweden.” Research in Transportation Economics 39(1):90–103.
Matusiewicz, M. 2020. “Logistics of the Future – Physical Internet and Its Practicality.” Transportation Journal 59 (2):200–14.
McKinnon, A.C., and Ge, Y. 2006. “The Potential for Reducing Empty Running by Trucks: A Retrospective Analysis.” International Journal of Physical Distribution & Logistics Management 36(5):391–410.
Meller, R.D., Montreuil, B., Thivierge, C., and Montreuil, Z. 2013. Functional Design of Physical Internet Facilities: A Road-Based Transit Center. Montreal, Canada: CIRRELT.
Mervis, J. 2014. “The information highway gets physical: The Physical Internet Would Move Goods the Way Its Namesake Moves Data.” Science 344(6188):1104–107.
MODULUSHCA 2016. Project Final Report: Modular Logistics Units in Shared Co-Modal Networks. Karlsruhe, Germany: PTV Group.
Mollenkopf, D., Closs, D., Twede, D., Lee, S., and Burgess, G. 2005. “Assessing the Viability of Reusable Packaging: A Relative Cost Approach.” Journal of Business Logistics 26 (1):169–97.
Montabon, F., Pagell, M., and Wu, Z. 2016. “Making Sustainability Sustainable.” Journal of Supply Chain Management 52(2):11–27.
Montreuil, B. 2011. “Toward a Physical Internet: Meeting the Global Logistics Sustainability Grand Challenge.” Logistics Research 3(2–3):71–87.
Montreuil, B., Ballot, E., and Tremblay, W. 2015. "Modular Design of Physical Internet Transport, Handling and Packaging Containers." Charlotte, NC: Progress in Material Handling Research.
Montreuil, B., Meller, R.D., Thivierge, C., and Montreuil, Z. 2013. Functional Design of Physical Internet Facilities: A Unimodal Road-based Crossdocking Hub. Montreal, Canada: CIRRELT.
Montreuil, B., Roug`es, J.-F., Cimon, Y., and Poulin, D. 2012. “The Physical Internet and Business Model Innovation.” Technology Innovation Management Review 2(6):32–37.
Pålsson, H., and Hellström, D. 2016. “Packaging Logistics in Supply Chain Practice – Current State, Trade-Offs and Improvement Potential.” International Journal of Logistics: Research and Applications 19(5):351–68.
Pålsson, H., and Sternberg, H. 2018. “High Capacity Vehicles and Modal Shift from Rail to Road: Combining Macro and Micro Analyses.” International Journal of Logistics: Research and Applications 21(2):115–32.
Pålsson, H., Winslott Hiselius, L., Wandel, S., Kahn, J., and Adell, E. 2017. “Longer and Heavier Road Freight Vehicles in Sweden – Effects on Tonne- and Vehicle-Kilometres, CO2 and Socio-Economics.” International Journal of Physical Distribution and Logistics Management 47(7):603–22.
Pan, S., Ballot, E., and Fontane, F. 2013. “The Reduction of Greenhouse Gas Emissions from Freight Transport by Pooling Supply Chains.” International Journal of Production Economics 143(1):86–94.
Pan, S., Ballot, E., Huang, G.Q., and Montreuil, B. 2017. “Physical Internet and Interconnected Logistics Services: Research and Applications.” International Journal of Production Research 55(9):2603–609.
160 H. S. Sternberg and M. Denizel Premkumar, G., Ramamurthy, K., and Crum, M. 1997. “Determinants of EDI Adoption in the Transport Industry.” European Journal of Information Systems 6(2):107–21.
Rai, H.B., Verlinde, S., Merckx, J., and Macharis, C. 2017. “Crowd Logistics: An Opportunity for More Sustainable Urban Freight Transport?” European Transport Research Review 9(3):39–52.
Rogers, D.S., Melamed, B., and Lembke, R.S. 2012. “Modeling and Analysis of Reverse Logistics.” Journal of Business Logistics 33(2):107–17.
Sallez, Y., Pan, S., Montreuil, B., Berger, T., and Ballot, E. 2016. “On the Activeness of Intelligent Physical Internet Containers.” Computers in Industry 81:96–104.
Salvador, F., Forza, C., and Rungtusanatham, M. 2002. “Modularity, Product Variety, Production Volume, and Component Sourcing: Theorizing beyond Generic Prescriptions.” Journal of Operations Management 20 (5):549–75.
Sandberg, K., Ado, A., Berntsson, S., Johansson, M., Melkersson, M., Petterson, H., Stelling, P., and Söderbaum, F. 2016. Godstransporter i Sverige – en nulägesanalys. edited by Brita Saxton. Stockholm, Sweden: Trafikanalys.
Sarraj, R., Ballot, E., Pan, S., Hakimi, D., and Montreuil, B. 2014a. “Interconnected Logistic Networks and Protocols: Simulation-based Efficiency Assessment.” International Journal of Production Research 52(11):3185–208.
Sarraj, R., Ballot, E., Pan, S., and Montreuil, B.. 2014b. “Analogies between Internet Network and Logistics Service Networks: Challenges Involved in the Interconnection.” Journal of Intelligent Manufacturing 25(6):1207–19.
Schilling, M.A. 2000. “Toward a General Modular Systems Theory and Its Application to Interfirm Product Modularity.” Academy of Management Review 25(2):312–34.
Shintani, K., Imai, A., Nishimura, E., and Papadimitriou, S. 2007. “The Container Shipping Network Design Problem with Empty Container Repositioning.” Transportation Research Part E: Logistics and Transportation Review 43 (1):39–59.
Simmer, L., Pfoser, S., Grabner, M., Schauer, O., and Putz, L.M. 2017. “From Horizontal Collaboration to the Physical Internet – A Case Study from Austria.” International Journal of Transport Development and Integration 1(2):129–36.
Song, D.-P. 2007. “Characterizing Optimal Empty Container Reposition Policy in Periodic-review Shuttle Service Systems.” Journal of the Operational Research Society 58 (1):122–33.
Stank, T.P., Pellathy, D.A., In, J., Mollenkopf, D.A., and Bell, J.E. 2017. “New Frontiers in Logistics Research: Theorizing at the Middle Range.” Journal of Business Logistics 38 (1):1–12.
Starr, M. 2010. “Modular Production – A 45-year-old Concept.” International Journal of Operations & Production Management 30(1):7–19.
Sternberg, H., and Norrman, A. 2017. “The Physical Internet – Review, Analysis and Future Research Agenda.” International Journal of Physical Distribution and Logistics Management 47(8):736–62.
Suzuki, Y., and Lu, S.-H. 2017. “Economies of Product Diversity in Collaborative Logistics.” Journal of Business Logistics 38(2):115–29.
Treiblmaier, H., Mirkovski, K., and Lowry, P.B. 2016. "Conceptualizing the Physical Internet: Literature Review, Implications and Directions for Future Research." 11th CSCMP Annual European Research Seminar, Vienna, Austria.
Treiblmaier, H, Mirkovski, K., Lowry, P.B., and Zacharia, Z.G. 2020. “The physical internet as a new supply chain paradigm: a systematic literature review and a comprehensive framework.” The International Journal of Logistics Management 31(2):239–87.
Tuunanen, T., Bask, A., and Merisalo-Rantanen, H. 2012. “Typology for Modular Service Design: Review of Literature.” International Journal of Service Science, Management, Engineering, and Technology 3(3):99–112.
Venkatesh, V., Morris, M.G., Davis, G.B., and Davis, F.D. 2003. “User Acceptance of Information Technology: Toward a Unified View.” MIS Quarterly 27(3):425–78.
Vierth, I., Mellin, A., Hyl´en, B., Karlsson, J., Karlsson, R., and Johansson, M. 2012. Kartläggning av godstransporterna i Sverige. In VTI Rapport. Linköping, Sweden: VTI.
Voss, C.A., Perks, H., Sousa, R., Witell, L., and Wünderlich, N.V. 2016. “Reflections on Context in Service Research.” Journal of Service Management 27(1):30–36.
Wall, J. 2013. Missing Link 2013. Gothenburg, Sweden: Ramböll.
Waller, M.A., and Fawcett, S.E. 2012. “Mathematical Modeling in Logistics: In for a Penny, in for a Pound.” Journal of Business Logistics 33(2):78–79.
Yang, Y., Pan, S., and Ballot, E. 2017. “Mitigating Supply Chain Disruption through Interconnected Logistics Services in the Physical Internet.” International Journal of Production Research 55(14):3970–83.
Yun, W.Y., Lee, Y.M., and Choi, Y.S. 2001. “Optimal Inventory Control of Empty Containers in Inland Transportation System.” International Journal of Production Economics 133 (1):451–57.


















